题目内容
某软件公司新开发一款学习软件,该软件把学科知识设计为由易到难共12关的闯关游戏.为了激发闯关热情,每闯过一关都奖励若干慧币(一种网络虚拟币).该软件提供了三种奖励方案:第一种,每闯过一关奖励40慧币;第二种,闯过第一关奖励4慧币,以后每一关比前一关多奖励4慧币;第三种,闯过第一关奖励0.5慧币,以后每一关比前一关奖励翻一番(即增加1倍),游戏规定:闯关者须于闯 关前任选一种奖励方案.
关前任选一种奖励方案.
(1)设闯过n(n∈N*,且n≤12)关后三种奖励方案获
 得的慧币依次为An,Bn,Cn,试求出An,Bn,Cn的表达式;
得的慧币依次为An,Bn,Cn,试求出An,Bn,Cn的表达式;
(2)如果你是一名闯关者,为了得到更多的慧币,你应如何选择奖励方案?
解:(1)第一种奖励方案闯过各关所得慧币构成常数列,∴An=40n,
第二种奖励方案闯过各关所得慧币构成首项是4,公差为4的等差数列,
∴Bn=4n+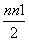 ×4=2n2+2n,
×4=2n2+2n,
第三种奖励方案闯过各关所得慧币构成首项是0.5,公比为2的等比数列,
∴Cn=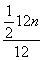 =
=
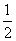 (2n
(2n -1
-1 ).
).
(2)令An>Bn,即40n>2n2+2n,解得n<19,
∵n∈N*,且 n≤12,∴An>Bn恒成立.
n≤12,∴An>Bn恒成立.
令An>Cn,即40n>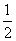 (2n-1),可得n<10,
(2n-1),可得n<10,
∴当n<10时,An最大;当10≤n≤12时, Cn>An.
综上,若我是一名闯关者,当能冲过的关数小于10时,应选用第一种奖励方案;当能冲过的关数大于等于10时,应选用第三种奖励方案.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 表示抽到评价该教师为“优秀”的人数,求
表示抽到评价该教师为“优秀”的人数,求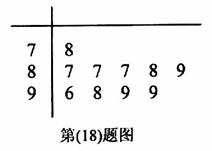
 (n
(n N)的展开式中,前三项的系数依次成等差数列,则此展开式有理项的项数是 。
N)的展开式中,前三项的系数依次成等差数列,则此展开式有理项的项数是 。  的解集为
的解集为 ,则
,则 的解集为(
的解集为( B.
B. C.
C. D.
D. 
 .
. 时解此不等式;
时解此不等式; ,此不等式恒成立,求实数
,此不等式恒成立,求实数 的取值范围.
的取值范围. B.
B.
 D.
D. 
 在x=1处有极值,则ab的最大值等于
在x=1处有极值,则ab的最大值等于 中
中 ,公比
,公比 ,记
,记 (即
(即 表示
表示 项之积),
项之积), ,
, ,
, ,
, 中值为正数的个数是
中值为正数的个数是 B.
B.  C.
C.  D.
D. 


 ,则
,则 的值为( )
的值为( )