题目内容
已知函数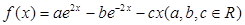 的导函数
的导函数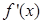 为偶函数,且曲线
为偶函数,且曲线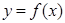 在点
在点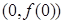 处的切线的斜率为
处的切线的斜率为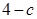 .
.
(1)确定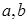 的值;
的值;
(2)若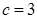 ,判断
,判断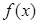 的单调性;
的单调性;
(3)若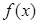 有极值,求
有极值,求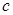 的取值范围.
的取值范围.
(1)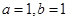 ;(2)增函数;(3)
;(2)增函数;(3)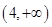 .
.
解析试题分析:(1)由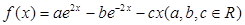
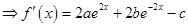
因为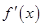 是偶函数,所以
是偶函数,所以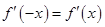 ,又曲线
,又曲线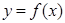 在点
在点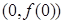 处的切线的斜率为
处的切线的斜率为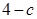 ,所以有
,所以有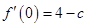 ,利用以上两条件列方程组可解
,利用以上两条件列方程组可解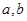 的值;
的值;
(2)由(1),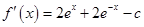 ,当
,当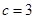 时,利用
时,利用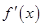 的符号判断
的符号判断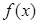 的单调性;
的单调性;
(3)要使函数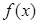 有极值,必须
有极值,必须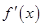 有零点,由于
有零点,由于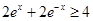 ,所以可以对
,所以可以对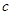 的取值分类讨论,得到时满足条件的
的取值分类讨论,得到时满足条件的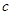 的取值范围.
的取值范围.
解:(1)对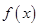 求导得
求导得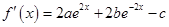 ,由
,由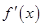 为偶函数,知
为偶函数,知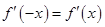 ,
,
即 ,因
,因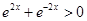 ,所以
,所以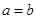
又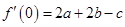 ,故
,故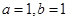 .
.
(2)当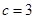 时,
时,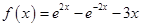 ,那么
,那么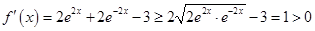
故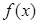 在
在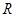 上为增函数.
上为增函数.
(3)由(1)知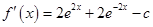 ,而
,而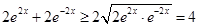 ,当
,当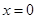 时等号成立.
时等号成立.
下面分三种情况进行讨论.
当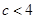 时,对任意
时,对任意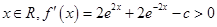 ,此时
,此时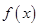 无极值;
无极值;
当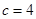 时,对任意
时,对任意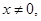
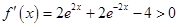 ,此时
,此时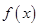 无极值;
无极值;
当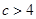 时,令
时,令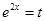 ,注意到方程
,注意到方程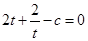 有两根,
有两根,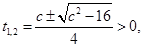
即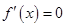 有两个根
有两个根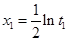 或
或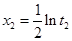 .
.
当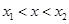 时,
时,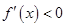 ;又当
;又当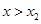 时,
时,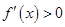 从而
从而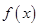 在
在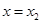 处取得极小值.
处取得极小值.
综上,若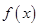 有极值,则
有极值,则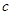 的取值范围为
的取值范围为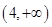 .
.
考点:1、导数的几何意义及导数在研究函数性质中的应用;2、分类讨论的思想.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
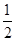 是函数f(x)=ln(x+1)-x+
是函数f(x)=ln(x+1)-x+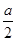 x2的一个极值点。
x2的一个极值点。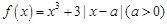 ,若
,若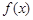 在
在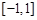 上的最小值记为
上的最小值记为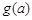 .
.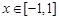 时,恒有
时,恒有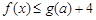 .
.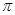 为圆周率,
为圆周率,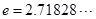 为自然对数的底数.
为自然对数的底数.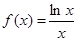 的单调区间;
的单调区间;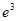 ,
,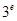 ,
,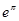 ,
,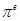 ,
, ,
,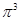 这6个数中的最大数与最小数;
这6个数中的最大数与最小数;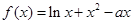 (
(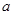 为常数).
为常数).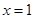 是函数
是函数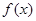 的一个极值点,求
的一个极值点,求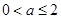 时,试判断
时,试判断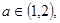
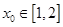 ,使不等式
,使不等式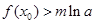 恒成立,求实数
恒成立,求实数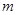 的取值范围.
的取值范围.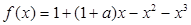 ,其中
,其中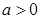 .
. 在其定义域上的单调性;
在其定义域上的单调性;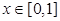 时,求
时,求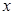 的值.
的值.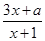 在区间[3,10]上封闭,求实数a的取值范围;
在区间[3,10]上封闭,求实数a的取值范围;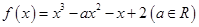 .
.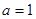 时,求函数
时,求函数 的极值;
的极值;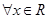 ,有
,有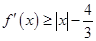 成立,求实数
成立,求实数 的取值范围.
的取值范围.