题目内容
设函数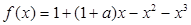 ,其中
,其中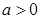 .
.
(1)讨论 在其定义域上的单调性;
在其定义域上的单调性;
(2)当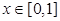 时,求
时,求 取得最大值和最小值时的
取得最大值和最小值时的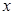 的值.
的值.
(1) 在
在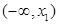 和
和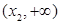 内单调递减,在
内单调递减,在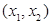 内单调递增;(2)所以当
内单调递增;(2)所以当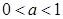 时,
时, 在
在 处取得最小值;当
处取得最小值;当 时,
时, 在
在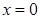 和
和 处同时取得最小只;当
处同时取得最小只;当 时,
时, 在
在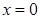 处取得最小值.
处取得最小值.
解析试题分析:(1)对原函数进行求导,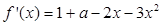 ,令
,令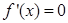 ,解得
,解得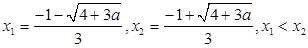 ,当
,当 或
或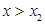 时
时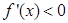 ;从而得出,当
;从而得出,当 时,
时,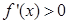 .故
.故 在
在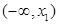 和
和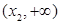 内单调递减,在
内单调递减,在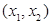 内单调递增.(2)依据第(1)题,对
内单调递增.(2)依据第(1)题,对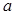 进行讨论,①当
进行讨论,①当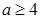 时,
时,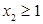 ,由(1)知,
,由(1)知, 在
在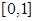 上单调递增,所以
上单调递增,所以 在
在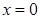 和
和 处分别取得最小值和最大值.②当
处分别取得最小值和最大值.②当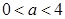 时,
时,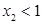 .由(1)知,
.由(1)知, 在
在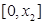 上单调递增,在
上单调递增,在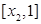 上单调递减,因此
上单调递减,因此 在
在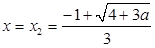 处取得最大值.又
处取得最大值.又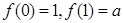 ,所以当
,所以当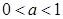 时,
时, 在
在 处取得最小值;当
处取得最小值;当 时,
时, 在
在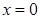 和
和 处同时取得最小只;当
处同时取得最小只;当 时,
时, 在
在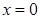 处取得最小值.
处取得最小值.
(1) 的定义域为
的定义域为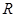 ,
,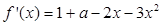 .令
.令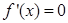 ,得
,得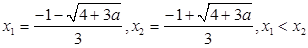 ,所以
,所以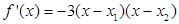 .当
.当 或
或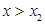 时
时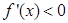 ;当
;当 时,
时,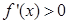 .故
.故 在
在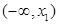 和
和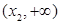 内单调递减,在
内单调递减,在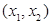 内单调递增.
内单调递增.
因为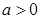 ,所以
,所以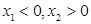 .
.
①当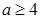 时,
时,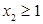 ,由(1)知,
,由(1)知, 在
在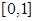 上单调递增,所以
上单调递增,所以 在
在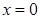 和
和 处分别取得最小值和最大值.②当
处分别取得最小值和最大值.②当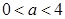 时,
时,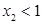 .由(1)知,
.由(1)知, 在
在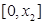 上单调递增,在
上单调递增,在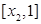 上单调递减,因此
上单调递减,因此 在
在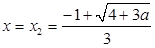 处取得最大值.又
处取得最大值.又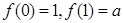 ,所以当
,所以当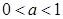 时,
时, 在
在 处取得最小值;当
处取得最小值;当 时,
时, 在
在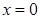 和
和 处同时取得最小只;当
处同时取得最小只;当
练习册系列答案
相关题目
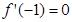 .
.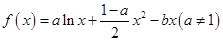 ,曲线
,曲线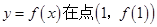 处的切线斜率为0
处的切线斜率为0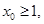 使得
使得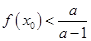 ,求a的取值范围。
,求a的取值范围。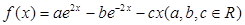 的导函数
的导函数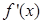 为偶函数,且曲线
为偶函数,且曲线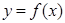 在点
在点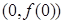 处的切线的斜率为
处的切线的斜率为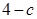 .
.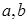 的值;
的值; 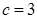 ,判断
,判断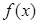 的单调性;
的单调性;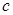 的取值范围.
的取值范围.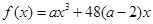 ,
,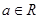 .若
.若
 的值;
的值;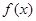 的单调区间及极值.
的单调区间及极值.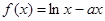 ,
,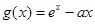 ,其中
,其中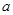 为实数,若
为实数,若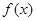 在
在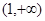 上是单调减函数,且
上是单调减函数,且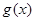 在
在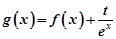 ,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;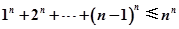 (n∈N*).
(n∈N*).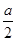 x2.
x2. x2-bx(b为常数).
x2-bx(b为常数).