题目内容
将边长 为的正方形ABCD沿对角线AC折起,使BD=
为的正方形ABCD沿对角线AC折起,使BD= ,则三棱锥
,则三棱锥 的体积为( )
的体积为( )
A. | B. | C. | D. |
D
解析试题分析:设点O是AC中点,连接DO,BO,△ADC,△ABC都是等腰直角三角形 ,则DO=B0= AC=
AC= ,BD=a,△BDO也是等腰直角三角形 ,DO⊥AC,DO⊥BO ,DO⊥平面ABC, DO就是三棱锥D-ABC的高,
,BD=a,△BDO也是等腰直角三角形 ,DO⊥AC,DO⊥BO ,DO⊥平面ABC, DO就是三棱锥D-ABC的高, ,故三棱锥D-ABC的体积
,故三棱锥D-ABC的体积 ,故选D
,故选D
考点:本题考查了三棱锥体积的求法
点评:弄清三棱锥的底面和高是求解此类问题的常用方法,有时还可根据等体积法求三棱锥的体积

练习册系列答案
相关题目
在一个几何体的三视图中,正视图和俯视图如下图所示,则该几何体的体积为( ) 
A. cm3( cm3( | B. cm3 cm3 | C. cm3 cm3 | D. cm3 cm3 |
若某多面体的三视图如图所示,则此多面体的体积是( )
| A.2 | B.4 | C.6 | D.12 |
若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( ) 

A.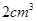 | B. |
C. | D. |
一个棱锥的三视图如图,则该棱锥的表面积(单位:c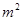 )为( )
)为( )
A.48+12 | B.48+24 | C.36+12 | D.36+24 |
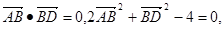 若将其沿BD折起,使平面ABD
若将其沿BD折起,使平面ABD 平面BDC则三棱锥A-BCD的外接球的表面积为:( )
平面BDC则三棱锥A-BCD的外接球的表面积为:( )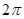



 的等腰三角形,侧视图是半径为1的半圆,则该几何体的体积是
的等腰三角形,侧视图是半径为1的半圆,则该几何体的体积是







 和直线
和直线 ,
, 所围成的平面图形,绕
所围成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 ;由同时满足
;由同时满足 ,
, ,
, ,
, 的点
的点 构成的平面图形,绕
构成的平面图形,绕 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察


