题目内容
在平行四边形ABCD中，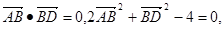
若将其沿BD折起，使平面ABD
平面BDC则三棱锥A-BCD的外接球的表面积为：（ ）
A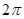． | B．4 | C． | D． |
B
解析试题分析：平行四边形ABCD中，∵
，∴AB⊥BD，沿BD折成直二面角A-BD-C，∵平面ABD⊥平面BDC，三棱锥A-BCD的外接球的直径为AC，∴
∴外接球的半径为1，故三棱锥A-BCD的外接球的表面积是4π．故选B
考点：本题考查了平面向量数量积的运算及球的性质
点评：对于球内接多面体问题，其中根据已知求出三棱锥A-BCD的外接球的半径是解答的关键
练习册系列答案
相关题目
以下对于几何体的描述，错误的是（ ）
| A．以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的旋转体叫做球 |
| B．一个等腰三角形绕着底边上的高所在直线旋转180º形成的封闭曲面所围成的图形叫做圆锥 |
| C．用平面去截圆锥，底面与截面之间的部分叫做圆台 |
| D．以矩形的一边所在直线为旋转轴，其余三边旋转形成的面所围成的旋转体叫做圆柱 |
如右图是某几何体的三视图，则此几何体的体积是( )
| A．36 | B．108 | C．72 | D．180 |
一个球的表面积是
，那么这个球的体积为（ ）
A． | B． | C． | D． |
将边长
为的正方形ABCD沿对角线AC折起，使BD=，则三棱锥
的体积为（ ）
A． | B． | C． | D． |
