题目内容
我国齐梁时代的数学家祖暅(公元前5-6世纪)提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等.
设:由曲线 和直线
和直线 ,
, 所围成的平面图形,绕
所围成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 ;由同时满足
;由同时满足 ,
, ,
, ,
, 的点
的点 构成的平面图形,绕
构成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察 可以得到
可以得到 的体积为
的体积为
A. | B. | C. | D. |
B
解析试题分析:根据题意,由于半个大球的体积减去了两个半个小球的体积即为的旋转体 的体积,即为
的体积,即为 ,故答案为B
,故答案为B
考点:祖暅原理,曲边梯形的面积
点评:理解体积的求解,根据祖暅原理求解等面积的平面图形对应的体积相等,有创意,培养同学们分析和解决问题能力。

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为 
| A.3 | B.6 |
| C.8 | D.12 |
图是一个几何体的三视图,根据图中数据,可得该几何体的表面积、体积分别是
A.32 、 、 | B.16 、 、 |
C.12 、 、 | D.8 、 、 |
将边长 为的正方形ABCD沿对角线AC折起,使BD=
为的正方形ABCD沿对角线AC折起,使BD= ,则三棱锥
,则三棱锥 的体积为( )
的体积为( )
A. | B. | C. | D. |
利用斜二测画法可以得到:
①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;
③正方形的直观图是正方形;④菱形的直观图是菱形. 以上结论正确的是( )
| A.①② | B.① | C.③④ | D.①②③④ |
某几何体的三视图如图所示,则它的体积是( )
A.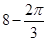 | B. |
C. | D. |





 ,则此四面体体积的最大值是
,则此四面体体积的最大值是

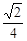

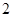 的正方形,两条虚线互相垂直,则该几何体的体积是( )
的正方形,两条虚线互相垂直,则该几何体的体积是( )



