题目内容
已知p:|1-
|≤2,q:x2-2x+1-m2≤0(m＞0),且
p是
q的必要不充分条件,求实数m的取值范围.
解法一：由x2-2x+1-m2≤0得1-m≤x≤1+m,
∴:A={x|x＞1+m或x＜1-m,m＞0}.
由|1-|≤2得-2≤x≤10,
∴:B={x|x＜-2或x＞10}.
∵
p是
q的必要而不充分条件,
∴A
B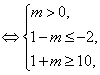
解得m≥9.
解法二：∵
p是
q的必要而不充分条件,
∴q是p的必要而不充分条件.
∴p是q的充分而不必要条件.
由x2-2x+1-m2≤0得1-m≤x≤1+m(m＞0).
∴q:Q={x|1-m≤x≤1+m,m＞0}.
又由|1-
|≤2得-2≤x≤10,
∴p:P={x|-2≤x≤10}.
∵p是q的充分而不必要条件,
∴P
Q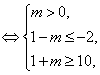
解得m≥9.
练习册系列答案
相关题目
|≤2,q:x2-2x+1-m2≤0(m>0),若
p是
q的充分不必要条件，求实数m的范围.
|≤2,q:x2-2x+1-a2≤0(a＞0),若
是
的充分不必要条件,求实数a的取值范围.
|≤2;q:x2-2x+1-m2≤0（m＞0），若﹁p是﹁q的充分不必要条件，求实数m的取值范围.
|≤2,q:x2-2x+1-m2≤(m＞0),若
p是
q的必要而不充分条件,求实数m的取值范围.
|≤2,q:x2-2x+1-m2≤0(m＞0),若
p是
q的充分而不必要条件，求实数m的取值范围.