题目内容
在直角坐标系xOy中，曲线C1的参数方程为
（t为参数）；以原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C2的极坐标方程为ρ=
．
（1）求曲线C1的普通方程与曲线C2的直角坐标方程；
（2）是判断曲线C1与C2是否存在两个交点，若存在求出两个交点间的距离；若不存在，说明理由．
|
| 2 | ||
|
（1）求曲线C1的普通方程与曲线C2的直角坐标方程；
（2）是判断曲线C1与C2是否存在两个交点，若存在求出两个交点间的距离；若不存在，说明理由．
考点：简单曲线的极坐标方程,参数方程化成普通方程
专题：坐标系和参数方程
分析：（1）直接把参数方程和极坐标方程转化成直角坐标方程．
（2）利用（1）的结论进一步联立方程组根据判别式和根和系数的关系，求出弦长．
（2）利用（1）的结论进一步联立方程组根据判别式和根和系数的关系，求出弦长．
解答：
解：（1）对于曲线曲线C1的参数方程
，转化成直角坐标方程为：x+y=1，
对于曲线C2的极坐标方程转化成直角坐标方程为：
+y2=1．
（2）显然曲线C1：x+y=1，则其参数方程可写为
①（t为参数）与曲线C2：
+y2=1②联立，
得到：
t2-6
t-4=0
所以：可知△＞0，所以C1与C2存在两个交点，
由t1+t2=
，t1t2=
，
得d=|t2-t1|=
=
．
|
对于曲线C2的极坐标方程转化成直角坐标方程为：
| x2 |
| 4 |
（2）显然曲线C1：x+y=1，则其参数方程可写为
|
| x2 |
| 4 |
得到：
| 5 |
| 2 |
| 2 |
所以：可知△＞0，所以C1与C2存在两个交点，
由t1+t2=
12
| ||
| 5 |
| 8 |
| 5 |
得d=|t2-t1|=
| (t1+t2)2-4t1t2 |
8
| ||
| 5 |
点评：本题考查的知识要点：参数方程和极坐标方程与直角坐标方程的转化，判别式的应用，根和系数的关系的应用，弦长公式的应用，属于基础题型．
练习册系列答案
相关题目
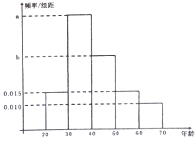根据某电子商务平台的调查统计显示，参与调查的1000为上网购物者的年龄情况如图所示：