题目内容
曲线 是平面内与定点
是平面内与定点 和定直线
和定直线 的距离的积等于
的距离的积等于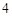 的点的轨迹.给出下列四个结论:
的点的轨迹.给出下列四个结论:
①曲线 过坐标原点;
过坐标原点;
②曲线 关于
关于 轴对称;
轴对称;
③曲线 与
与 轴有
轴有 个交点;
个交点;
④若点 在曲线
在曲线 上,则
上,则 的最小值为
的最小值为 .
.
其中,所有正确结论的序号是___________.
 是平面内与定点
是平面内与定点 和定直线
和定直线 的距离的积等于
的距离的积等于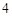 的点的轨迹.给出下列四个结论:
的点的轨迹.给出下列四个结论:①曲线
 过坐标原点;
过坐标原点;②曲线
 关于
关于 轴对称;
轴对称;③曲线
 与
与 轴有
轴有 个交点;
个交点;④若点
 在曲线
在曲线 上,则
上,则 的最小值为
的最小值为 .
.其中,所有正确结论的序号是___________.
①②④
试题分析:设
 曲线
曲线 上任意一点,则依题意可得
上任意一点,则依题意可得 ,将原点代入验证,方程成立,说明曲线
,将原点代入验证,方程成立,说明曲线 过坐标原点,故①正确;把方程中的x不变,y被-y 代换,方程不变,说明曲线
过坐标原点,故①正确;把方程中的x不变,y被-y 代换,方程不变,说明曲线 关于
关于 轴对称,故②正确;将
轴对称,故②正确;将 代入方程
代入方程 可得
可得 ,即方程只有一个根,所以③不正确;定点
,即方程只有一个根,所以③不正确;定点 和定直线
和定直线 可看做是抛物线
可看做是抛物线 的焦点和准线,设点
的焦点和准线,设点 是抛物线上的任意一点,由抛物线的定义可知点
是抛物线上的任意一点,由抛物线的定义可知点 到焦点和准线的距离相等,要使
到焦点和准线的距离相等,要使 的最小值画图分析可知点
的最小值画图分析可知点 应在抛物线
应在抛物线 的内侧且
的内侧且 ,当点
,当点 在
在 上时
上时 取得最小值,此时
取得最小值,此时 ,点
,点 到直线
到直线 的距离为
的距离为 ,所以
,所以 ,解得
,解得 ,此时
,此时 。故④正确。综上可得正确的是①②④。
。故④正确。综上可得正确的是①②④。
练习册系列答案
相关题目
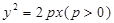 ,其准线方程为
,其准线方程为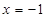 ,过准线与
,过准线与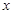 轴的交点
轴的交点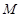 做直线
做直线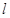 交抛物线于
交抛物线于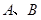 两点.
两点.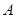 为
为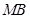 中点,求直线
中点,求直线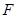 ,当
,当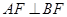 时,求
时,求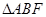 的面积.
的面积. :
: (
( )过点
)过点 ,且椭圆
,且椭圆 .
. 在直线
在直线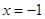 上,过
上,过 两点,且
两点,且 中点,再过
中点,再过 .证明:直线
.证明:直线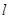 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.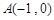 ,
,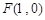 ,动点
,动点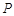 满足
满足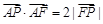 .
.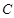 的方程;
的方程;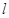 :
: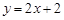 上取一点
上取一点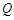 ,过点
,过点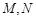 .问:是否存在点
.问:是否存在点 //
// :
: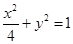 .
.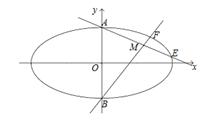
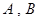 (如图),直线
(如图),直线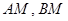 分别与椭圆
分别与椭圆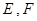 两点,其中点
两点,其中点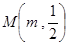 满足
满足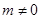 ,且
,且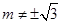 .
.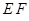 与
与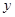 轴交点的位置与
轴交点的位置与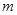 无关;
无关;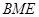 面积是∆
面积是∆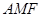 面积的5倍,求
面积的5倍,求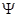 :
: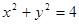 .
.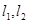 是过点
是过点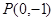 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中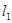 交圆
交圆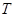 、
、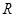 两点,
两点,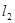 交椭圆
交椭圆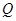 .求
.求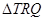 面积取最大值时直线
面积取最大值时直线 =1(a>b>0)上两点,已知m=
=1(a>b>0)上两点,已知m= ,n=
,n= ,若m·n=0且椭圆的离心率e=
,若m·n=0且椭圆的离心率e= ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点. ,
, 分别为双曲线
分别为双曲线
 ,
, 的左、右焦点,若在右支上存在点
的左、右焦点,若在右支上存在点 ,使得点
,使得点 到直线
到直线 的距离为
的距离为 ,则该双曲线的离心率的取值范围是( )
,则该双曲线的离心率的取值范围是( )



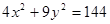 内有一点
内有一点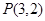 ,过点
,过点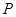 的弦恰好以
的弦恰好以 中,
中, 为侧面
为侧面 所在平面上的一个动点,且
所在平面上的一个动点,且 的距离是
的距离是 距离的
距离的 倍,则动点
倍,则动点