题目内容
已知函数 (
(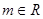 ),
),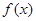 的导数为
的导数为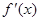 ,且
,且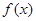 的图像过点
的图像过点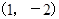
(1)求函数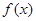 的解析式;
的解析式;
(2)设函数 ,若
,若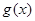 在
在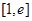 的最小值是2,求实数
的最小值是2,求实数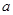 的值.
的值.
 (
(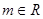 ),
),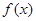 的导数为
的导数为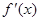 ,且
,且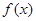 的图像过点
的图像过点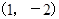
(1)求函数
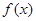 的解析式;
的解析式;(2)设函数
 ,若
,若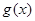 在
在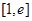 的最小值是2,求实数
的最小值是2,求实数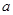 的值.
的值.解:(1)由已知得

 ……………………………………………2分
……………………………………………2分
 …………4分
…………4分(2)

 …………………6分
…………………6分①
 ,
,
 …………8分
…………8分②


 ……10分
……10分③


综上所述
 …………………………………………………………………12分
…………………………………………………………………12分本试题主要是考查了导数的求解最值,和运用导数和原函数的关系求解析式。

练习册系列答案
相关题目

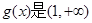 上的增函数,求k的取值范围;
上的增函数,求k的取值范围; 求满足条件的最大整数k的值。
求满足条件的最大整数k的值。 。
。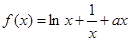 (
(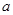 为实数).
为实数).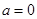 时, 求
时, 求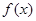 的最小值;
的最小值;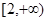 上是单调函数,求
上是单调函数,求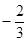 与x=1时都取得极值.
与x=1时都取得极值.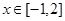 ,不等式f(x)<c2恒成立,求c的取值范围.
,不等式f(x)<c2恒成立,求c的取值范围.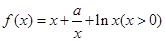 ,其中
,其中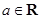 .
.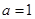 时,求
时,求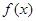 的单调递增区间;
的单调递增区间;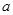 的取值范围,使得对任意的
的取值范围,使得对任意的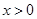 ,都有
,都有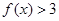 .
.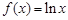 ,
,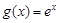 .
.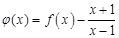 ,求函数
,求函数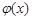 的单调区间;
的单调区间; 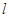 为函数
为函数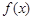 的图象上一点
的图象上一点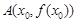 处的切线.证明:在区间
处的切线.证明:在区间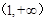 上存在唯一的
上存在唯一的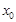 ,使得直线
,使得直线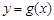 相切.
相切.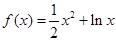 .
.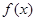 在区间
在区间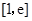 上的最大、最小值;
上的最大、最小值;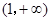 上,函数
上,函数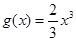 的图象的下方
的图象的下方 ,存在
,存在 ,
, ,则
,则 的最大值为 。
的最大值为 。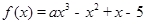 在区间
在区间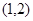 上单调递增,则a的范围为__ ____.
上单调递增,则a的范围为__ ____.