题目内容
设函数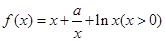 ,其中
,其中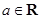 .
.
(1)当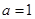 时,求
时,求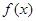 的单调递增区间;
的单调递增区间;
(2)求实数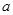 的取值范围,使得对任意的
的取值范围,使得对任意的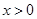 ,都有
,都有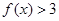 .
.
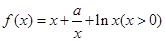 ,其中
,其中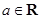 .
.(1)当
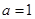 时,求
时,求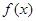 的单调递增区间;
的单调递增区间;(2)求实数
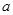 的取值范围,使得对任意的
的取值范围,使得对任意的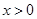 ,都有
,都有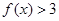 .
.(1)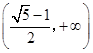 ;(2)
;(2)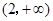
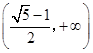 ;(2)
;(2)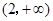
(1)求导,根据导数大于零,求其单调增区间.
(2)解本题关键是做好以下转化:对任意的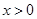 ,都有
,都有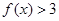 ,即
,即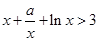 ,
,
则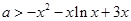 . 设函数
. 设函数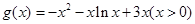 ,则要使对任意的
,则要使对任意的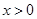 ,都有
,都有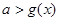 ,须且只须
,须且只须 .
.
解:(1)当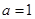 时,
时,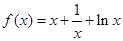 ,则
,则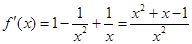 , ……2分
, ……2分
由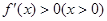 ,得
,得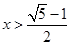 , ………………………………………………4分
, ………………………………………………4分
所以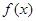 的单调递增区间为
的单调递增区间为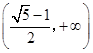 ;……………………………………………6分
;……………………………………………6分
(2) 对任意的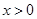 ,都有
,都有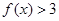 ,即
,即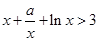 ,
,
则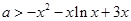 . ………………8分
. ………………8分
设函数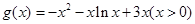 ,则要使对任意的
,则要使对任意的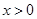 ,都有
,都有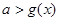 ,须且只须
,须且只须 .下面求
.下面求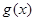 的最大值. ………………10分
的最大值. ………………10分
易得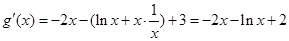 ,
,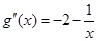 ,
,
由于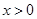 ,故
,故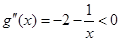 ,于是
,于是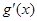 在
在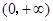 内单调递减,
内单调递减,
注意到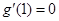 ,故当
,故当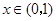 时,
时,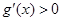 ;当
;当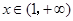 时,
时,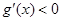 ,
,
因此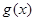 在
在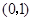 内单调递增,在
内单调递增,在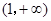 内单调递减, ……………13分
内单调递减, ……………13分
从而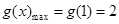 .
.
所以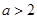 ,即所求的实数
,即所求的实数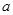 的取值范围是
的取值范围是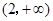 . ……………15分.
. ……………15分.
(2)解本题关键是做好以下转化:对任意的
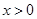 ,都有
,都有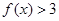 ,即
,即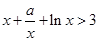 ,
,则
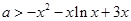 . 设函数
. 设函数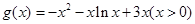 ,则要使对任意的
,则要使对任意的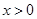 ,都有
,都有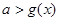 ,须且只须
,须且只须 .
.解:(1)当
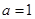 时,
时,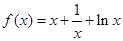 ,则
,则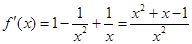 , ……2分
, ……2分由
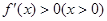 ,得
,得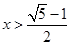 , ………………………………………………4分
, ………………………………………………4分所以
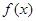 的单调递增区间为
的单调递增区间为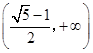 ;……………………………………………6分
;……………………………………………6分(2) 对任意的
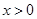 ,都有
,都有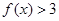 ,即
,即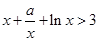 ,
,则
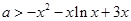 . ………………8分
. ………………8分设函数
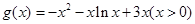 ,则要使对任意的
,则要使对任意的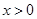 ,都有
,都有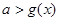 ,须且只须
,须且只须 .下面求
.下面求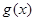 的最大值. ………………10分
的最大值. ………………10分易得
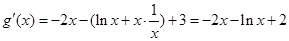 ,
,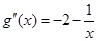 ,
,由于
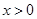 ,故
,故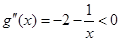 ,于是
,于是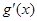 在
在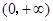 内单调递减,
内单调递减,注意到
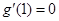 ,故当
,故当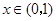 时,
时,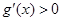 ;当
;当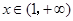 时,
时,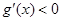 ,
,因此
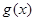 在
在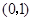 内单调递增,在
内单调递增,在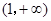 内单调递减, ……………13分
内单调递减, ……………13分从而
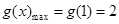 .
.所以
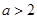 ,即所求的实数
,即所求的实数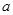 的取值范围是
的取值范围是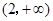 . ……………15分.
. ……………15分.
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
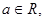 函数
函数 。
。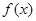 在区间
在区间 上最小值
上最小值 ;
;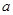 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数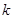 的取值范围;
的取值范围;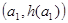 ,B
,B ,C
,C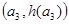 ,从左到右依次是函数
,从左到右依次是函数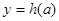 图象上三点,且这三点不共线,求证:
图象上三点,且这三点不共线,求证: 是钝角三角形。
是钝角三角形。 (
(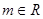 ),
),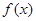 的导数为
的导数为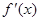 ,且
,且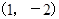
 ,若
,若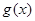 在
在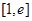 的最小值是2,求实数
的最小值是2,求实数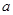 的值.
的值.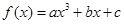 在
在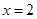 处取得极值为
处取得极值为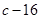
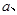
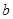 的值;(2)若
的值;(2)若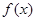 有极大值28,求
有极大值28,求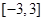 上的最小值.
上的最小值.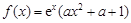
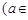 R).
R).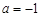 ,求曲线
,求曲线 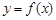 在点
在点 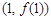 处的的切线方程;
处的的切线方程;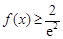 对任意
对任意 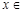
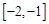 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
 时,求曲线
时,求曲线 处的切线方程;
处的切线方程; 时,求
时,求 的极大值和极小值;
的极大值和极小值; 上是增函数,求实数
上是增函数,求实数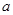 的取值范围.
的取值范围.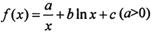 的图象在点(1, f(1))处的切线方程为x-y-2=0
的图象在点(1, f(1))处的切线方程为x-y-2=0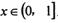 上的最大值为2,求实数a的取值范围.
上的最大值为2,求实数a的取值范围.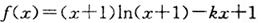 ,,k为常数,e是自然对数的底数).
,,k为常数,e是自然对数的底数).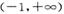 上的图象均在第一、二象限?若存在,求出k的最大值;若不存在,请说明理由;
上的图象均在第一、二象限?若存在,求出k的最大值;若不存在,请说明理由;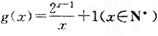 ,记
,记 ,求证:
,求证: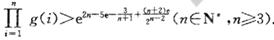
 的单调递增区间是
的单调递增区间是