题目内容
1．下列说法中错误的是（ ）| A． | y=cosx在[2kπ，2kπ+$\frac{π}{2}$]（k∈Z）上是减函数 | |
| B． | y=cosx在[-π，0]上是增函数 | |
| C． | y=cosx在第一象限是减函数 | |
| D． | y=sinx和y=cosx在[$\frac{π}{2}$，π]上都是减函数 |
分析 根据三角函数的单调性，分别进行判断即可．
解答 解：A．y=cosx在[2kπ，2kπ+$\frac{π}{2}$]（k∈Z）上是减函数，正确，
B．y=cosx在[-π，0]上是增函数，正确
C．=cosx在第一象限内不具备单调性，故C错误，
D．y=sinx和y=cosx在[$\frac{π}{2}$，π]上都是减函数，正确，
故选：C．
点评 本题主要考查命题的真假判断，涉及三角函数的单调性的性质，难度不大．
练习册系列答案
相关题目
11．已知函数y=f（x-l）+x2是定义在R上的奇函数，若f（-2）=1，则f（0）=（ ）
| A． | -3 | B． | -2 | C． | -1 | D． | 0 |
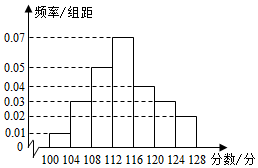某校高三（1）班在一次单元测试中，每位同学的考试分数都在区间[100，128]内，将该班所有同学的考试分数分为七组：[100，104），[104，108），[108，112），[112，116），[116，120），[120，124），[124，128]，绘制出频率分布直方图如图所示，已知分数低于112分的有18人，则分数不低于120分的人数为（ ）
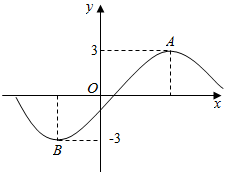已知函数f（x）=3sin（ωx+φ）（ω＞0，|φ|≤$\frac{π}{2}$）的部分图象如图所示，A、B两点之间的距离为10，且f（2）=0，若将函数f（x）的图象向右平移t（t＞0）个单位长度后所得函数图象关于y轴对称，则t的最小值为6．
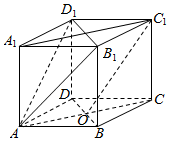在直平行六面体ABCD-A1B1C1D1中，底面ABCD是菱形，∠DAB=60°，AC∩BD=O，AB=AA1=1．