题目内容
10.求曲线xy=1在点P(x0,y0)处的切线与两坐标轴围成的三角形的面积.分析 由xy=1即y=$\frac{1}{x}$,求得导数,求得切线的斜率和切点,由点斜式方程可得切线的方程,分别令x=0,y=0得到y,x轴的截距,运用三角形的面积公式计算即可得到所求值.
解答 解:xy=1即y=$\frac{1}{x}$的导数为y′=-$\frac{1}{{x}^{2}}$,
即有曲线点P(x0,y0)处的切线的斜率为k=-$\frac{1}{{{x}_{0}}^{2}}$,
切点为(x0,$\frac{1}{{x}_{0}}$),
可得点P(x0,y0)处的切线的方程为y-$\frac{1}{{x}_{0}}$=-$\frac{1}{{{x}_{0}}^{2}}$(x-x0),
令x=0可得,y=$\frac{2}{{x}_{0}}$;令y=0可得x=2x0,
即有切线与两坐标轴围成的三角形的面积为S=$\frac{1}{2}$•|2x0|•|$\frac{2}{{x}_{0}}$|=2.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义,正确求导和运用点斜式方程是解题的关键,属于基础题.

练习册系列答案
相关题目
1.设x∈[0,3],执行如图所示的程序框图,从输出的结果中随机取一个数a,“2a-10≥0”的概率为( )
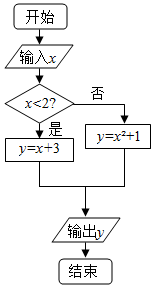

| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{5}{7}$ | D. | $\frac{4}{7}$ |
15.若向量$\overrightarrow{a}$⊥$\overrightarrow{b}$,则一定有( )
| A. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| | B. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | C. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$| | D. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| |
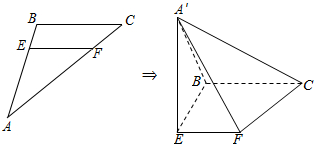 已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AE=2EB,AF=2FC,将△AEF沿EF折起,使A变到A′,使平面A′EF⊥平面EFCB.
已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AE=2EB,AF=2FC,将△AEF沿EF折起,使A变到A′,使平面A′EF⊥平面EFCB.
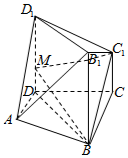 如图,几何体ABCD-B1C1D1中,正方形BB1D1D⊥平面ABCD,D1D∥CC1,平面D1DCC1与平面B1BCC1所成的二面角的余弦值为$\frac{2}{3}$,BC=3,CD=2CC1=2,AD=$\sqrt{5}$,AD∥BC,M为DD1上任意一点.
如图,几何体ABCD-B1C1D1中,正方形BB1D1D⊥平面ABCD,D1D∥CC1,平面D1DCC1与平面B1BCC1所成的二面角的余弦值为$\frac{2}{3}$,BC=3,CD=2CC1=2,AD=$\sqrt{5}$,AD∥BC,M为DD1上任意一点.