题目内容
点P是圆x2+y2=1上的动点,它与定点(3,0)的连线段的中点的轨迹方程是
- A.

- B.
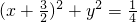
- C.(x+3)2+y2=4
- D.(x-3)2+y2=4
A
分析:设出线段中点的坐标,利用中点坐标公式,求出P的坐标,代入的方程即可确定线段中点的轨迹方程.
解答:设线段中点的坐标为(x,y),P的坐标(a,b),
因为线段的中点是P与(3,0)的中点,
所以满足 ,
,
所以 ,
,
因为P是圆x2+y2=1上的动点,
所以(2x-3)2+(2y)2=1,
即: ,
,
所以所求线段的中点的轨迹方程是 .
.
故选A.
点评:本题是中档题,考查曲线的轨迹方程的求法,注意所求点的坐标与动点坐标的关系是解题的关键,考查转化思想,计算能力.
分析:设出线段中点的坐标,利用中点坐标公式,求出P的坐标,代入的方程即可确定线段中点的轨迹方程.
解答:设线段中点的坐标为(x,y),P的坐标(a,b),
因为线段的中点是P与(3,0)的中点,
所以满足
 ,
,所以
 ,
,因为P是圆x2+y2=1上的动点,
所以(2x-3)2+(2y)2=1,
即:
 ,
,所以所求线段的中点的轨迹方程是
 .
.故选A.
点评:本题是中档题,考查曲线的轨迹方程的求法,注意所求点的坐标与动点坐标的关系是解题的关键,考查转化思想,计算能力.

练习册系列答案
相关题目
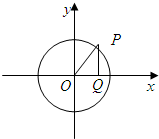 已知点P是圆x2+y2=1上的一个动点,过点P作PQ⊥x轴于点Q,设
已知点P是圆x2+y2=1上的一个动点,过点P作PQ⊥x轴于点Q,设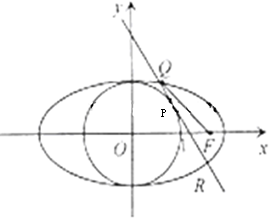 已知椭圆C:
已知椭圆C: