Question

【题目】已知圆 ，圆心为 ，定点 ， 为圆 上一点，线段 上一点 满足 ，直线 上一点 ，满足 ．
（Ⅰ）求点 的轨迹 的方程；
（Ⅱ） 为坐标原点， 是以 为直径的圆，直线 与 相切，并与轨迹 交于不同的两点 ．当 且满足 时，求 面积 的取值范围．

Answer 1

【答案】解：（Ⅰ）∵
∴ 为线段 中点
∵
∴ 为线段 的中垂线
∴
∵
∴由椭圆的定义可知 的轨迹是以 为焦点，长轴长为 的椭圆，
设椭圆的标准方程为 ，
则 ， ，
∴ 。
∴点 的轨迹 的方程为 。
（Ⅱ）∵圆 与直线 相切，
∴ ，即 ，
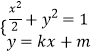由 ，消去 .
∵直线 与椭圆交于两个不同点，
∴ ，
将 代入上式，可得 ，
设 ， ，
则 ， ，
∴ ，
∴
∴ ，
∵ ，解得 .满足 。
又 ，
设 ，则 .
∴ ，
∴
故 面积 的取值范围为 。
【解析】（1）根据题意易得QN为线段的中垂线，可得，所以，由椭圆的定义可知Q的轨迹是以为焦点，长轴长为的椭圆。
（2）由直线 l : y = k x + m 与 ⊙ O 相切可得=1即。将该式与Q的轨迹C的方程联立整理后得，可以表示出，又直线 l 与椭圆交于两个不同点，根据题目中λ的范围和这个条件可求出k的范围。，根据求出的k的范围即可求出S的取值范围。