题目内容
如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<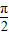 )的图象的一段.
)的图象的一段.(1)试确定函数f(x)=Asin(ωx+φ)的解析式.
(2)求函数g(x)=
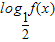 的单调递减区间.并利用图象判断方程f(x)=3lgx解的个数.
的单调递减区间.并利用图象判断方程f(x)=3lgx解的个数.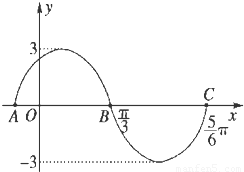
【答案】分析:(1)由图可知A=3,利用其周期为π,可求得ω,再利用y=f(x)过(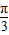 ,0)可求得φ,从而可得函数f(x)=Asin(ωx+φ)的解析式;
,0)可求得φ,从而可得函数f(x)=Asin(ωx+φ)的解析式;
(2)利用复合函数的单调性,只需求f(x)=3sin(2x+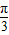 )>0的单调递增区间即可;作出y=3lgx与f(x)=3sin(2x+
)>0的单调递增区间即可;作出y=3lgx与f(x)=3sin(2x+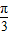 )的图象即可求得答案.
)的图象即可求得答案.
解答:解:(1)由图知A=3, T=
T=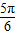 -
-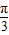 =
=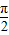 ,
,
∴T=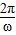 =π,
=π,
∴ω=2,
又2×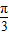 +φ=π,
+φ=π,
∴φ=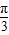
∴f(x)=3sin(2x+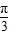 ).
).
(2)∵g(x)=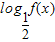 =
=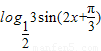 是复合函数,外层的对数函数单调递减,
是复合函数,外层的对数函数单调递减,
∴f(x)=3sin(2x+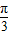 )>0且单调递增,
)>0且单调递增,
∴2kπ<2x+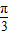 <2kπ+
<2kπ+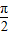 ,k∈Z,
,k∈Z,
∴kπ-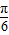 <x<kπ+
<x<kπ+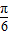 ,k∈Z.
,k∈Z.
∴g(x)=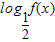 的单调递减区间为(kπ-
的单调递减区间为(kπ-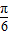 ,kπ+
,kπ+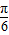 )k∈Z.
)k∈Z.
在同一直角坐标系中作出y=3lgx与f(x)=3sin(2x+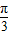 )的图象,
)的图象,
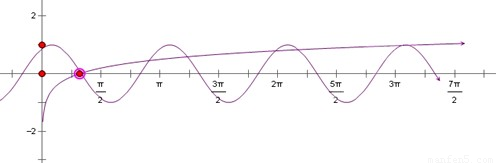
由图可知,两函数图象有7个交点,故方程f(x)=3lgx有7个解.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查根的存在性及根的个数判断,考查复合函数的单调性,作图是难点,属于难题.
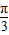 ,0)可求得φ,从而可得函数f(x)=Asin(ωx+φ)的解析式;
,0)可求得φ,从而可得函数f(x)=Asin(ωx+φ)的解析式;(2)利用复合函数的单调性,只需求f(x)=3sin(2x+
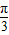 )>0的单调递增区间即可;作出y=3lgx与f(x)=3sin(2x+
)>0的单调递增区间即可;作出y=3lgx与f(x)=3sin(2x+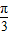 )的图象即可求得答案.
)的图象即可求得答案.解答:解:(1)由图知A=3,
 T=
T=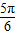 -
-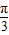 =
=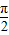 ,
,∴T=
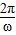 =π,
=π,∴ω=2,
又2×
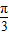 +φ=π,
+φ=π,∴φ=
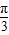
∴f(x)=3sin(2x+
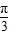 ).
).(2)∵g(x)=
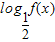 =
=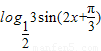 是复合函数,外层的对数函数单调递减,
是复合函数,外层的对数函数单调递减,∴f(x)=3sin(2x+
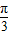 )>0且单调递增,
)>0且单调递增,∴2kπ<2x+
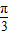 <2kπ+
<2kπ+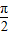 ,k∈Z,
,k∈Z,∴kπ-
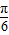 <x<kπ+
<x<kπ+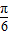 ,k∈Z.
,k∈Z.∴g(x)=
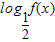 的单调递减区间为(kπ-
的单调递减区间为(kπ-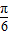 ,kπ+
,kπ+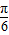 )k∈Z.
)k∈Z.在同一直角坐标系中作出y=3lgx与f(x)=3sin(2x+
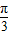 )的图象,
)的图象,
由图可知,两函数图象有7个交点,故方程f(x)=3lgx有7个解.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查根的存在性及根的个数判断,考查复合函数的单调性,作图是难点,属于难题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
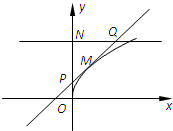 如图为函数f(x)=
如图为函数f(x)=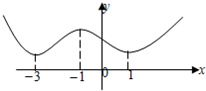
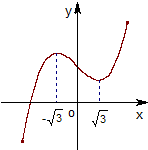 如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为
如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为 如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为( )
如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为( )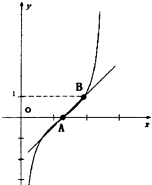 如图为函数f(x)=tan(
如图为函数f(x)=tan(