题目内容
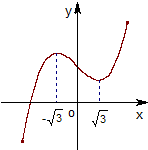 如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为
如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为分析:先从原函数的极值点处得出导数的零点,再利用导函数是二次函数的特点,结合二次函数的图象,即可解出不等式x•f′(x)<0的解集.
解答: 解:由图可知:
解:由图可知:
±
是函数f(x)=ax3+bx2+cx+d的两个极值点,且a>0
即±
是导函数f′(x)的两个零点,
导函数的图象如图,
由图得:
不等式x•f′(x)<0的解集为:
(-∞,-
)∪(0,
).
故答案为:(-∞,-
)∪(0,
).
 解:由图可知:
解:由图可知:±
| 3 |
即±
| 3 |
导函数的图象如图,
由图得:
不等式x•f′(x)<0的解集为:
(-∞,-
| 3 |
| 3 |
故答案为:(-∞,-
| 3 |
| 3 |
点评:本小题主要考查函数的图象、一元二次不等式的解法、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图为函数f(x)=
如图为函数f(x)=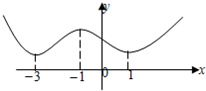
 如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为( )
如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为( ) 如图为函数f(x)=tan(
如图为函数f(x)=tan(