题目内容
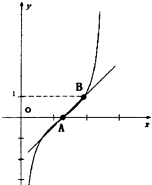 如图为函数f(x)=tan(
如图为函数f(x)=tan(| π |
| 4 |
| π |
| 2 |
分析:根据正切函数的性质求出A,B的坐标,利用直线斜率和倾斜角之间的关系即可得到结论.
解答:解:由
x-
=kπ,得x=2+4k,k∈Z,
∵点A为函数f(x)在y轴右侧的第一个零点,
∴当k=0时,x=2,即A(2,0).
由f(x)=tan(
x-
)=1,
得
x-
=
,即x=3,
∴B(3,1),
直线AB的斜率k=
=1,
即直线AB的倾斜角等于45°,
故答案为:45°.
| π |
| 4 |
| π |
| 2 |
∵点A为函数f(x)在y轴右侧的第一个零点,
∴当k=0时,x=2,即A(2,0).
由f(x)=tan(
| π |
| 4 |
| π |
| 2 |
得
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
∴B(3,1),
直线AB的斜率k=
| 1-0 |
| 3-2 |
即直线AB的倾斜角等于45°,
故答案为:45°.
点评:本题主要考查直线斜率和倾斜角的计算,根据正切函数求出A,B的坐标是解决本题的关键.

练习册系列答案
相关题目
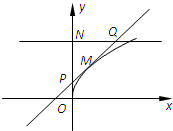 如图为函数f(x)=
如图为函数f(x)=
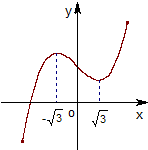 如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为
如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为 如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为( )
如图为函数f(x)=ax3+bx2+cx+d的图象,f′(x)为函数f(x)的导函数,则不等式x•f′(x)<0的解集为( )