��Ŀ����
��֪����Ϊq(0��q��1)������ȱ�����{an}����ĺ�Ϊ9������ȱ�����{a2n}����ĺ�Ϊ(1)������{an}������a1����q;
(2)�Ը�����k(k=1,2,��,n)����T(k)������Ϊak������Ϊ2ak-1�ĵȲ����У�������T(2)��ǰ10��֮�ͣ�
(3)��biΪ����T(i)�ĵ�i�Sn=b1+b2+��+bn����Sn������������m(m��1)��ʹ��![]()
![]() �����Ҳ�������.
�����Ҳ�������.
(ע������ȱ����и���ĺͼ���n����ʱ������ȱ�����ǰn��͵ļ���)
�⣺(1)�������֪��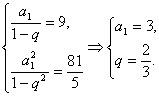
(2)��(1)֪��an=3��(![]() )n-1����������T(2)������Ϊt1=a2=2������d=2a2-1=3��
)n-1����������T(2)������Ϊt1=a2=2������d=2a2-1=3��
S10=10��2+![]() ��10��9��3=155.������T(2)��ǰ10��֮��Ϊ155.
��10��9��3=155.������T(2)��ǰ10��֮��Ϊ155.
(3)bi=ai+(i-1)(2ai-1)=(2i-1)ai-(i-1)=3(2i-1)(![]() )i-1-(i-1)��
)i-1-(i-1)��
Sn=45-(18n+27)(![]() )n-
)n-![]() ��
��
![]()
![]() =
=![]() -
-![]() (
(![]() )n-
)n-![]() .
.
��m=2ʱ��![]()
![]() =-
=-![]() ;��m��2ʱ��
;��m��2ʱ��![]()
![]() =0������m=2.
=0������m=2.

��ϰ��ϵ�д�
�����Ŀ
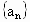 ����ĺ�Ϊ9������ȱ�����
����ĺ�Ϊ9������ȱ�����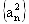 ����ĺ�Ϊ
����ĺ�Ϊ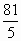 ��
��
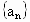 ������
������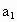 ����q��
����q��
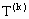 ������Ϊ
������Ϊ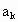 ������Ϊ
������Ϊ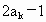 �ĵȲ����У�������
�ĵȲ����У�������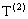 ��ǰ10��֮�ͣ�
��ǰ10��֮�ͣ�
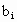 ����
Ϊ���� �ĵ�i�
�ĵ�i�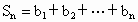 ����
����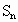 ������������m(m��1)��ʹ��
������������m(m��1)��ʹ��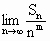 �����Ҳ������㣮
�����Ҳ������㣮
 ʱ������ȱ�����ǰn��͵ļ���)
ʱ������ȱ�����ǰn��͵ļ���)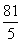 ��
��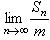 �����Ҳ������㡣
�����Ҳ������㡣