题目内容
点O在△ABC内,满足
+2
+3
=
,那么△AOB与△AOC的面积之比是( )
| OA |
| OB |
| OC |
| 0 |
| A、2:1 | B、3:2 |
| C、3:1 | D、5:3 |
考点:向量加减混合运算及其几何意义
专题:平面向量及应用
分析:画出图形,结合图形,作出平行四边形OAFE,使得
=2
,根据题意,求出S△ABC=2S△AOB,S△ABC=3S△AOC,从而得出答案来.
| OE |
| OB |
解答:
解:如图所示,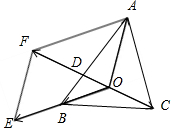
延长OB到点E,使得
=2
,
分别以
、
为邻边作平行四边形OAFE,
则
+
=
,
+2
=
;
∵
+2
+3
=
,
∴
=-3
;
又∵
=
=2
,
∴
=2
;
∴
=3
,
∴
=-
,
∴S△ABC=2S△AOB;
同理可得:S△ABC=3S△AOC,
∴△AOB,△AOC的面积比为3:2.

延长OB到点E,使得
| OE |
| OB |
分别以
| OA |
| OE |
则
| OA |
| OE |
| OF |
| OA |
| OB |
| OF |
∵
| OA |
| OB |
| OC |
| 0 |
∴
| OF |
| OC |
又∵
| AF |
| OE |
| OB |
∴
| DF |
| OD |
∴
| OF |
| OD |
∴
| OD |
| OC |
∴S△ABC=2S△AOB;
同理可得:S△ABC=3S△AOC,
∴△AOB,△AOC的面积比为3:2.
点评:本题考查了平面向量的合成法则、向量共线定理以及三角形的面积计算公式的应用问题,解题时应画出图形,认真分析,是较难的题目.

练习册系列答案
相关题目
i是虚数单位,复数z=1+
在复平面内对应的点位于( )
| 1 |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
cos(-240°)的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
下表是某厂1到4月份用水量情况(单位:百吨)的一组数据:
用水量y与月份x之间具有线性相关关系,其线性回归方程为
=-0.7x+a,则a的值为( )
| 月份x | 1 | 2 | 3 | 4 |
| 用水量ym3 | 4.5 | 4 | 3 | 2.5 |
| ∧ |
| y |
| A、5.25 | B、5 |
| C、2.5 | D、3.5 |
已知函数f(x)=
,则满足f(x)≤2的x的取值范围是( )
|
| A、[-1,2] |
| B、[0,2] |
| C、[1,+∞) |
| D、[-1,+∞) |
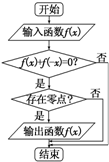 某流程图如图所示,现输入如下四个函数
某流程图如图所示,现输入如下四个函数