题目内容
已知直线l1:2x-ay+1=0,直线l2:4x+6y-7=0.
(1)若l1∥l2,求 a的值;
(2)若l1与l2相交,交点纵坐标为正数,求a的范围.
(1)若l1∥l2,求 a的值;
(2)若l1与l2相交,交点纵坐标为正数,求a的范围.
考点:直线的一般式方程
专题:直线与圆
分析:(1)因为l1∥l2,由A1B2-A2B1=0,能求出a的值.
(2)联立方程组
,得y=
,a≠-3,由已知得2a+6>0,由此能求出a的范围.
(2)联立方程组
|
| 9 |
| 2a+6 |
解答:
解:(1)因为l1∥l2,由A1B2-A2B1=0,
得2×6-(-a)×4=0,
解得a=-3.(6分)
(2)联立方程组
,
解得y=
,a≠-3.(8分)
由已知得2a+6>0,解得a>-3.(11分)
即a的范围为(-3,+∞).(12分)
得2×6-(-a)×4=0,
解得a=-3.(6分)
(2)联立方程组
|
解得y=
| 9 |
| 2a+6 |
由已知得2a+6>0,解得a>-3.(11分)
即a的范围为(-3,+∞).(12分)
点评:本题考查实数值的求法,是基础题,解题时要认真审题,注意直线的位置关系的合理运用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知函数g(x)=ax+a,f(x)=
,若对任意的x1∈[-2,2],存在x2∈[-2,2],使g(x1)=f(x2)成立,则a的取值范围是( )
|
A、[-
| ||
B、[-
| ||
| C、(0,1] | ||
| D、(-∞,1] |
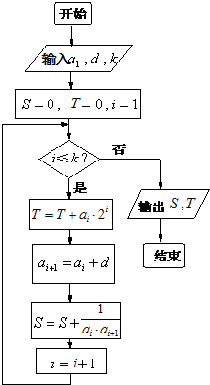 如图所示,程序框图给出了无穷正项数列{an}满足的条件,且当k=5时,输出的S是
如图所示,程序框图给出了无穷正项数列{an}满足的条件,且当k=5时,输出的S是 设y=f(x)为定义在R上的偶函数,当x≤-1时,y=f(x)的图象是经过点(-2,2),斜率为-1的一条射线,又当x∈[-1,0]时,y=f(x)的图象是顶点在(0,2),且过点(-1,1)的一段抛物线.
设y=f(x)为定义在R上的偶函数,当x≤-1时,y=f(x)的图象是经过点(-2,2),斜率为-1的一条射线,又当x∈[-1,0]时,y=f(x)的图象是顶点在(0,2),且过点(-1,1)的一段抛物线.