题目内容

用五点法作出函数y=sin4x+cos4x的简图,并求其定义域、值域,取最值时x的取值集合.

解:y=sin4x+cos4x

=(sin2x+cos2x)2-2sin2xcos2x

=1-sin22x=1-·

=+cos4x.

    列表(找五个关键点)

x

0

4x

0

π

2π

cos4x

1

0

-1

0

1

y

1

1

    利用余弦函数的性质描点画图.

    将右面位于区间［0, ］内的图象依次向左或向右平移个单位,即得函数在(-∞,+∞)上的图象.

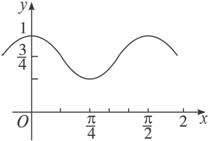
    易知函数的定义域为R,值域为［,1］,且y取最大值1时相应的x的值集为{x|x=,k∈Z}.y取最小值时相应的x的值集为{x|x=+,k∈Z}.

练习册系列答案
相关题目
用五点法作出函数y=3sin(2x+
π3
)在一个周期上的图象．
用五点法作出函数y=2sin(x+
π3
)在一个周期内的简图．
用“五点法”作出函数y=2sin(x-
π
4
)在长度为一个周期的闭区间的图象．
（1）列表
（2）作图
已知函数f(x)=2sin(x+
π
6
)-2cosx
（1）用五点法作出函数y=f（x）一个周期内的图象；
（2）当x∈[
π
2
，π]时，观察图象并写出函数f（x）的单调区间及函数的值域．
已知向量
a
=(sin(x-
π
4
)，-1)，
b
=(2，2)且f(x)=
a
•
b
+2
①用“五点法”作出函数y=f（x）在长度为一个周期的闭区间的图象．
②求函数f（x）的最小正周期和单调增区间；
③求函数f（x）的最大值，并求出取得最大值时自变量x的取值集合
④函数f（x）的图象可以由函数y=sin2x（x∈R）的图象经过怎样的变换得到？
⑤当x∈[0，π]，求函数y=2sin(x-
π
4
)的值域
解：（1）列表
（2）作图
精英家教网

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网