题目内容
“a≥0”是“函数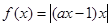
在区间（－∞，0）内单调递减”的（ ）
A.充要条件 B.必要不充分条件
C.充分不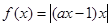必要条件
D.即不充分也不必要条件
【答案】
A
【解析】
试题分析：令t=（ax-1）x=ax2-x,则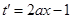
，设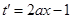=0，解得x=
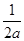，所以，当a≥0时，函数t=（ax-1）x在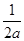（－∞，）上是减函数，在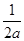（，+∞）上是增函数，即极小值为－
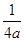，当x<0时，t>0,所以a≥0时，函数
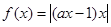在区间（－∞，0）内单调递减；若函数 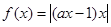在区间（－∞，0）内单调递减，则x
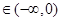时，
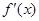<0,即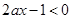
成立,所以2a ≥0，故选A.
考点：1.导数的应用；2.充分必要条件的判断.
练习册系列答案
相关题目