题目内容
求证:
(1)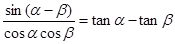
(2)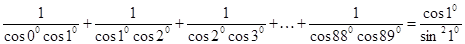
(1)
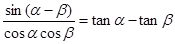
(2)
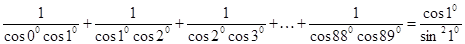
证明见解析.
试题分析:三角恒等式的证明也遵循从繁化简的原则,当然三角函数还有函数名称的转化与角的转化.(1)本题从左向右变化,首先把左边分子用两角差的正弦公式展开,就能证明,当然也可从右向左转化(切化弦),
 ;(2)这个证明要求我们善于联想,首先左边的和怎么求?能否变为两数的差(利用裂项相消的思想方法)?这个想法实际上在第(1)小题已经为我们做了,只要乘以
;(2)这个证明要求我们善于联想,首先左边的和怎么求?能否变为两数的差(利用裂项相消的思想方法)?这个想法实际上在第(1)小题已经为我们做了,只要乘以 (因为每个分母上的两角的差都是
(因为每个分母上的两角的差都是 ),每个分式都化为两数的差,而且恰好能够前后项相消.
),每个分式都化为两数的差,而且恰好能够前后项相消.试题解析:证明:(1)
 3分
3分 6分
6分(2)由(1)得
 (
( ) 8分
) 8分可得

 10分
10分 12分
12分即
 . 14分
. 14分
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 为锐角,
为锐角, ,
, ,求
,求 的值.
的值. ;
; ;
; ;
; ;
; .
. ).
). 的最大值,并写出
的最大值,并写出 ,b+c=2,求实数a的最小值。
,b+c=2,求实数a的最小值。
 ·
· +S的最大值;
+S的最大值; 的值.
的值.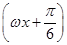 (其中ω>0,x∈R)的最小正周期为10π.
(其中ω>0,x∈R)的最小正周期为10π.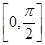 ,f
,f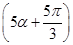 =-
=-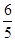 ,f
,f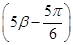 =
=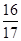 ,求cos(α+β)的值.
,求cos(α+β)的值. 中,
中,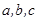 是角A,B,C的对边,若
是角A,B,C的对边,若 ,则
,则 ( )
( )



 且
且 则
则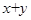 的可能取值是( )
的可能取值是( ) B
B 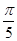 C.
C.  D.
D. 
 ,那么
,那么 的值是( )
的值是( )


