题目内容
已知数列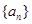 的各项均为正数,
的各项均为正数,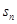 为其前
为其前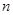 项和,对于任意的
项和,对于任意的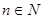 ,满足关系式
,满足关系式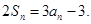
(1)求数列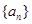 的通项公式;
的通项公式;
(2)设数列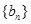 的通项公式是
的通项公式是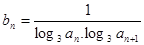 ,前
,前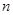 项和为
项和为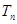 ,求证:对于任意的正整数n,总有
,求证:对于任意的正整数n,总有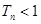
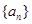 的各项均为正数,
的各项均为正数,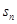 为其前
为其前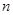 项和,对于任意的
项和,对于任意的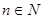 ,满足关系式
,满足关系式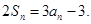
(1)求数列
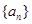 的通项公式;
的通项公式;(2)设数列
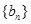 的通项公式是
的通项公式是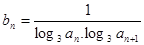 ,前
,前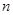 项和为
项和为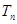 ,求证:对于任意的正整数n,总有
,求证:对于任意的正整数n,总有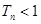
(1)
(2)根据列项求和法来得到数列的前n项和 进而证明。
进而证明。

(2)根据列项求和法来得到数列的前n项和
 进而证明。
进而证明。试题分析:
解:(1)由已知得

故
 , 即
, 即
故数列
 为等比数列,且
为等比数列,且
又当
 时,
时,

而
 亦适合上式
亦适合上式 
(2)

所以



点评:主要是考查了等比数列的通项公式和裂项法求和的综合运用,属于基础题。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
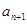 ,
,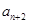 …的最小值记为Bn,dn=An-Bn.
…的最小值记为Bn,dn=An-Bn.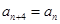 ),写出d1,d2,d3,d4的值;
),写出d1,d2,d3,d4的值; 的前n项和
的前n项和 ,且
,且 ,且
,且 成公比不等于1的等比数列。
成公比不等于1的等比数列。 ,求数列{
,求数列{ }的前n项和Tn.
}的前n项和Tn.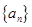 、
、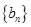 满足:
满足: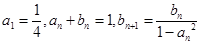 .
.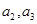 ;
;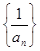 为等差数列,并求数列
为等差数列,并求数列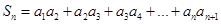 ,求实数
,求实数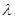 为何值时
为何值时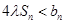 恒成立。
恒成立。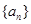 中,已知
中,已知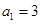 ,公比
,公比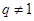 ,等差数列
,等差数列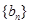 满足
满足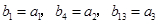 .
.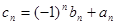 ,求数列
,求数列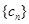 的前2n项和.
的前2n项和.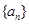 中,
中,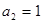 ,则其前
,则其前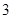 项的和
项的和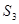 的取值范围是
的取值范围是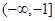
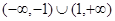
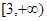
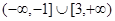
 中,如果
中,如果
 ( )
( ) ,则
,则 =( ).
=( ).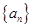 为等比数列,
为等比数列,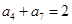 ,
,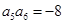 ,则
,则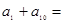 .
.