题目内容
直线 与圆
与圆 交于不同的两点
交于不同的两点 ,
, 为坐标原点,若
为坐标原点,若 ,则
,则 的值为( )
的值为( )
 与圆
与圆 交于不同的两点
交于不同的两点 ,
, 为坐标原点,若
为坐标原点,若 ,则
,则 的值为( )
的值为( )A. | B. | C. | D. |
B
分析:设A(x1,y1),B(x2,y2),把直线 代入圆x2+y2=1,应用韦达定理,代入两个向量数量积公式 进行运算求值.
代入圆x2+y2=1,应用韦达定理,代入两个向量数量积公式 进行运算求值.
解答:解:设A(x1,y1),B(x2,y2),把直线 代入圆x2+y2=1,得
代入圆x2+y2=1,得 ,因为直线与圆有交点,所以
,因为直线与圆有交点,所以 ,即
,即
由韦达定理得x1x2= ,同理可得 y1y2=
,同理可得 y1y2=
故 = x1x2+ y1y2 =
= x1x2+ y1y2 =
解得, ,又
,又 ,得
,得
故选B.
点评:本题考查直线和圆相交的性质,以及两个向量数量积公式的应用.
 代入圆x2+y2=1,应用韦达定理,代入两个向量数量积公式 进行运算求值.
代入圆x2+y2=1,应用韦达定理,代入两个向量数量积公式 进行运算求值.解答:解:设A(x1,y1),B(x2,y2),把直线
 代入圆x2+y2=1,得
代入圆x2+y2=1,得 ,因为直线与圆有交点,所以
,因为直线与圆有交点,所以 ,即
,即
由韦达定理得x1x2=
 ,同理可得 y1y2=
,同理可得 y1y2=
故
 = x1x2+ y1y2 =
= x1x2+ y1y2 =
 ,又
,又 ,得
,得
故选B.
点评:本题考查直线和圆相交的性质,以及两个向量数量积公式的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,圆
,圆 与
与 关于直线
关于直线 对称,则圆
对称,则圆

 .
.
 B = 90°,AC = 4,BC =
B = 90°,AC = 4,BC = 2,点P为线段CA(不包括端点)上的一个动点,以
2,点P为线段CA(不包括端点)上的一个动点,以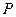 为圆心,1为半径作
为圆心,1为半径作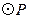 .
.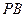 ,若
,若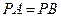 ,试判断
,试判断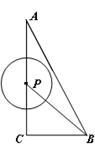
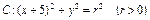 和直线
和直线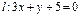 . 若圆
. 若圆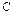 与直线
与直线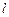 没有公共点,则
没有公共点,则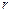 的取值范围是
的取值范围是 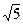 ,1)直线
,1)直线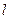 :
: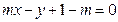
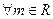 ,直线
,直线 点;
点;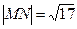 时,求m的值。
时,求m的值。 应该使它与球有最大的接触面积,问圆轴的半径x应是多少?
应该使它与球有最大的接触面积,问圆轴的半径x应是多少?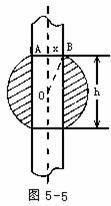
 为圆
为圆 内异于圆心的一点,则直线
内异于圆心的一点,则直线 与该圆的位置关系为
与该圆的位置关系为  .求 圆C的方程.
.求 圆C的方程. 与圆
与圆 相交于P、Q两点,且点P、Q关于直线
相交于P、Q两点,且点P、Q关于直线 对称,则不等式组
对称,则不等式组 表示的平面区域的面积为________
表示的平面区域的面积为________