题目内容
14. 如图所示,在边长为1的等边△ABC中,AA1=BB1=CC1=x(0<x<1),△A1B1C1的面积为y.
如图所示,在边长为1的等边△ABC中,AA1=BB1=CC1=x(0<x<1),△A1B1C1的面积为y.(1)试写出y与x的函数关系式;
(2)求y的最小值.
分析 (1)由三角形面积公式得y=${S}_{△ABC}-3{S}_{△{A}_{1}B{B}_{1}}$,由此能求出y与x的函数关系式.
(2)推导出y=$\frac{3\sqrt{3}}{4}$(x-$\frac{1}{2}$)2+$\frac{\sqrt{3}}{16}$,当x=$\frac{1}{2}$时,y取最小值ymin=$\frac{\sqrt{3}}{16}$.
解答 解:(1)∵在边长为1的等边△ABC中,
AA1=BB1=CC1=x(0<x<1),△A1B1C1的面积为y.
∴y=${S}_{△ABC}-3{S}_{△{A}_{1}B{B}_{1}}$=$\frac{1}{2}×1×1×sin60°$-3×$\frac{1}{2}×x×(1-x)×sin60°$
=$\frac{\sqrt{3}}{4}$-$\frac{3\sqrt{3}}{4}$x(1-x)=$\frac{3\sqrt{3}}{4}{x}^{2}-\frac{3\sqrt{3}}{4}x$+$\frac{\sqrt{3}}{4}$,
∴y与x的函数关系式为y=$\frac{3\sqrt{3}}{4}{x}^{2}-\frac{3\sqrt{3}}{4}x$+$\frac{\sqrt{3}}{4}$,(0<x<1).
(2)∵y=$\frac{3\sqrt{3}}{4}{x}^{2}-\frac{3\sqrt{3}}{4}x$+$\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{4}$(3x2-3x+1)
=$\frac{3\sqrt{3}}{4}$(x-$\frac{1}{2}$)2+$\frac{\sqrt{3}}{16}$.
∴当x=$\frac{1}{2}$时,y取最小值ymin=$\frac{\sqrt{3}}{16}$.
点评 本题考查三角函数恒等式、三角函数的周期、单调区间等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | 54种 | B. | 48种 | C. | 42种 | D. | 36种 |
| A. | 15°≤θ≤90° | B. | 60°≤θ≤90° | C. | 15°≤θ≤105° | D. | 30°≤θ≤105° |
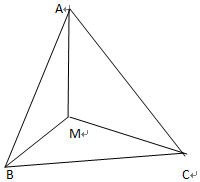 如图,等边△ABC中,AB=2,M为△ABC内一动点,∠BMC=120°;
如图,等边△ABC中,AB=2,M为△ABC内一动点,∠BMC=120°;