题目内容
等差数列{an} 的前n项的和为Sn,且S5=45,S6=60.
(1)求{an} 的通项公式;
(2)若数列{bn} 满足bn-bn=an-1(n∉N*),且b1=3,设数列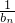 的前n项和为Tn.求证:Tn<
的前n项和为Tn.求证:Tn< .
.
(1)解:a6=S6-S5=15,由 =60,
=60,
解得a1=5,又∵d= =2,
=2,
所以an=2n+3.…4
(2)证明:∵b2-b1=a1,
b3-b2=a2,
b4-b3=a3,
…
bn-bn-1=an-1,
叠加得 =
= ,
,
所以 .…(9分)
.…(9分)
∴ ,
,
∴
=
= .…(12分)
.…(12分)
分析:(1)a6=S6-S5=15,由 =60,解得a1=5,再由d=
=60,解得a1=5,再由d= =2,能求出{an} 的通项公式.
=2,能求出{an} 的通项公式.
(2)由b2-b1=a1,b3-b2=a2,b4-b3=a3,…,bn-bn-1=an-1,叠加得 =
= ,所以
,所以 .
. ,由裂项求和法能够证明Tn<
,由裂项求和法能够证明Tn< .
.
点评:本题考查数列通项公式和数列前n项和的求法,证明Tn< .解题时要认真审题,注意等差数列通项公式的应用和裂项求和法的灵活运用.
.解题时要认真审题,注意等差数列通项公式的应用和裂项求和法的灵活运用.
 =60,
=60,解得a1=5,又∵d=
 =2,
=2,所以an=2n+3.…4
(2)证明:∵b2-b1=a1,
b3-b2=a2,
b4-b3=a3,
…
bn-bn-1=an-1,
叠加得
 =
= ,
,所以
 .…(9分)
.…(9分)∴
 ,
,∴

=

=
 .…(12分)
.…(12分)分析:(1)a6=S6-S5=15,由
 =60,解得a1=5,再由d=
=60,解得a1=5,再由d= =2,能求出{an} 的通项公式.
=2,能求出{an} 的通项公式.(2)由b2-b1=a1,b3-b2=a2,b4-b3=a3,…,bn-bn-1=an-1,叠加得
 =
= ,所以
,所以 .
. ,由裂项求和法能够证明Tn<
,由裂项求和法能够证明Tn< .
.点评:本题考查数列通项公式和数列前n项和的求法,证明Tn<
 .解题时要认真审题,注意等差数列通项公式的应用和裂项求和法的灵活运用.
.解题时要认真审题,注意等差数列通项公式的应用和裂项求和法的灵活运用. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目