题目内容
已知椭圆E的两个焦点分别为F1(-1,0),F2(1,0),点(1,
)在椭圆E上.
(1)求椭圆E的方程
(2)若椭圆E上存在一点 P,使∠F1PF2=30°,求△PF1F2的面积.
| 3 |
| 2 |
(1)求椭圆E的方程
(2)若椭圆E上存在一点 P,使∠F1PF2=30°,求△PF1F2的面积.
(1)设椭圆E的方程为
+
=1(a>b>0).
∵c=1,
∴a2-b2=1①,
∵点(1,
)在椭圆E上,
∴
+
=1②,
由①、②得:a2=4,b2=3,
∴椭圆E的方程为:
+
=1.
(2)由题意知,a=2,b=
、∴c=1
又∵点P在椭圆上,∴|PF1|+|PF2|=2a=4、①
由余弦定理知:|PF1|2+|PF2|2-2|PF1||PF2|cos30°=|F1F2|2=(2c)2=4②
把①两边平方得|PF1|2+|PF2|2+2|PF1|•|PF2|=16,③
③-②得(2+
)|PF1|•|PF2|=12,
∴|PF1|•|PF2|=12(2-
),
∴S△PF1F2=
|PF1|•|PF2|sin30°=6-3
、
| x2 |
| a2 |
| y2 |
| b2 |
∵c=1,
∴a2-b2=1①,
∵点(1,
| 3 |
| 2 |
∴
| 1 |
| a2 |
| 9 |
| 4b2 |
由①、②得:a2=4,b2=3,
∴椭圆E的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)由题意知,a=2,b=
| 3 |
又∵点P在椭圆上,∴|PF1|+|PF2|=2a=4、①
由余弦定理知:|PF1|2+|PF2|2-2|PF1||PF2|cos30°=|F1F2|2=(2c)2=4②
把①两边平方得|PF1|2+|PF2|2+2|PF1|•|PF2|=16,③
③-②得(2+
| 3 |
∴|PF1|•|PF2|=12(2-
| 3 |
∴S△PF1F2=
| 1 |
| 2 |
| 3 |

练习册系列答案
相关题目
 )在椭圆E上.
)在椭圆E上.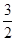 )在椭圆E上.
)在椭圆E上.