题目内容
（2007•广州二模）已知椭圆E的两个焦点分别为F1（-1，0）、F2（1，0），点C(1，
)在椭圆E上．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若点P在椭圆E上，且满足
•
=t，求实数t的取值范围．
| 3 |
| 2 |
（Ⅰ）求椭圆E的方程；
（Ⅱ）若点P在椭圆E上，且满足
| PF1 |
| PF2 |
分析：（Ⅰ）解法一：设椭圆E的方程为
+
=1（a＞b＞0），由半焦距c=1，a2-b2=1，点C（1，
）在椭圆E上，得到
+
=1．求出a2，b2，推出椭圆E的方程．
解法二：设椭圆E的方程为
+
=1（a＞b＞0），通过点C（1，
）在椭圆E上，利用2a=|CF1|+|CF2|，求出a=2．由已知半焦距c=1，求出b2．然后求出椭圆E的方程．
（Ⅱ）设P（x0，y0），由
•
=t，推出x02+y02=t+1．点P在曲线C上，
+
=1，得y02=t+1-x02，然后求出0≤x02≤4，解出2≤t≤3．得到实数t的取值范围．
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| a2 |
| 9 |
| 4b2 |
解法二：设椭圆E的方程为
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
（Ⅱ）设P（x0，y0），由
| PF1 |
| PF2 |
| ||
| 4 |
| ||
| 3 |
解答：（本小题满分14分）
（Ⅰ）解法一：依题意，设椭圆E的方程为
+
=1（a＞b＞0），
由已知半焦距c=1，∴a2-b2=1． ①…（2分）
∵点C（1，
）在椭圆E上，则
+
=1． ②…（4分）
由①、②解得，a2=4，b2=3．
∴椭圆E的方程为
+
=1． …（6分）
解法二：依题意，设椭圆E的方程为
+
=1（a＞b＞0），
∵点C（1，
）在椭圆E上，∴2a=|CF1|+|CF2|，即a=2． …（3分）
由已知半焦距c=1，∴b2=a2-c2=3． …（5分）
∴椭圆E的方程为
+
=1． …（6分）
（Ⅱ）设P（x0，y0），由
•
=t，得
（-1-x0．-y0）•（1-x0，-y0）=t，
即x02+y02=t+1． ③…（8分）
∵点P在曲线C上，
∴
+
=1． ④
由③得y02=t+1-x02，代入④，并整理得
x02=4（t-2）． ⑤…（10分）
由④知，0≤x02≤4，⑥…（12分）
结合⑤、⑥，解得：2≤t≤3．
∴实数t的取值范围为[2，3]． …（14分）
（Ⅰ）解法一：依题意，设椭圆E的方程为
| x2 |
| a2 |
| y2 |
| b2 |
由已知半焦距c=1，∴a2-b2=1． ①…（2分）
∵点C（1，
| 3 |
| 2 |
| 1 |
| a2 |
| 9 |
| 4b2 |
由①、②解得，a2=4，b2=3．
∴椭圆E的方程为
| x2 |
| 4 |
| y2 |
| 3 |
解法二：依题意，设椭圆E的方程为
| x2 |
| a2 |
| y2 |
| b2 |
∵点C（1，
| 3 |
| 2 |
由已知半焦距c=1，∴b2=a2-c2=3． …（5分）
∴椭圆E的方程为
| x2 |
| 4 |
| y2 |
| 3 |
（Ⅱ）设P（x0，y0），由
| PF1 |
| PF2 |
（-1-x0．-y0）•（1-x0，-y0）=t，
即x02+y02=t+1． ③…（8分）
∵点P在曲线C上，
∴
| ||
| 4 |
| ||
| 3 |
由③得y02=t+1-x02，代入④，并整理得
x02=4（t-2）． ⑤…（10分）
由④知，0≤x02≤4，⑥…（12分）
结合⑤、⑥，解得：2≤t≤3．
∴实数t的取值范围为[2，3]． …（14分）
点评：本小题主要考查椭圆的概念、椭圆的方程等基础知识，考查待定系数法、数形结合的数学思想与方法，以及运算求解能力．
练习册系列答案
阅读快车系列答案
相关题目
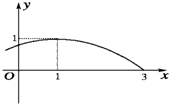（2007•广州二模）函数f（x）=sin（ωx+?），（x∈R，ω＞0，0≤?＜2π）的部分图象如图所示，则ω=
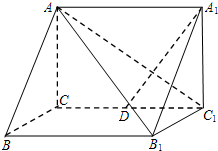（2007•广州二模）如图所示，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AB=2，BC=1，