题目内容
【题目】选修4-4：坐标系与参数方程
已知过点
的直线
的参数方程是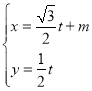
（
为参数）．以平面直角坐标系的原点为极点，
轴的正半轴为极轴，建立极坐标系，曲线
的极坐标方程式为
.
（Ⅰ）求直线的普通方程和曲线
的直角坐标方程；
（Ⅱ）若直线与曲线
交于两点
，且
，求实数
的值．
【答案】（Ⅰ）
：
，C：
．（Ⅱ）
或1．
【解析】
试题分析：（Ⅰ）用消参数法可化参数方程为普通方程，由公式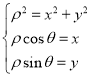
可化极坐标方程为直角坐标方程；（Ⅱ）题中参数方程是过P点的直线的标准参数方程，参数t具有几何意义，
表示直线上的点到P点的距离，因此只要把直线参数方程代入曲线C的直角坐标方程，由韦达定理易得．
试题解析：（Ⅰ）直线的参数方程是
，（
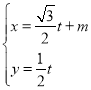为参数），
消去参数
可得．
由
，得
，
可得
的直角坐标方程：．
（Ⅱ）把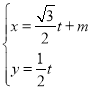
（
为参数），代入
，
得
，
由
，解得
．
∴
．
∵
，∴
，
解得
或1．又满足
．∴实数或1．
练习册系列答案
相关题目
【题目】《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20～80mg/100ml（不含80）之间，属于酒后驾车；在80mg/100ml（含80）以上时，属于醉酒驾车．某市公安局交通管理部门在某路段的一次拦查行动中，依法检查了300辆机动车，查处酒后驾车和醉酒驾车的驾驶员共20人，检测结果如表：
酒精含量（mg/100ml） | [20，30） | [30，40） | [40，50） | [50，60） | [60，70）[] | [70，80） | [80，90） | [90，100] |
人数 | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
（Ⅰ）绘制出检测数据的频率分布直方图（在图中用实线画出矩形框即可）；
（Ⅱ）求检测数据中醉酒驾驶的频率，并估计检测数据中酒精含量的众数、平均数．
