题目内容
已知椭圆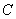 :
: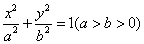 的离心率为
的离心率为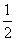 ,右焦点
,右焦点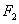 到直线
到直线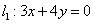 的距离为
的距离为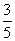 .
.
(Ⅰ)求椭圆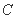 的方程;
的方程;
(Ⅱ)过椭圆右焦点F2斜率为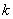 (
(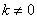 )的直线
)的直线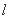 与椭
与椭 圆
圆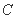 相交于
相交于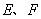 两点,
两点,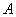 为椭圆的右顶点,直线
为椭圆的右顶点,直线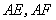 分别交直线
分别交直线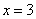 于点
于点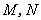 ,线段
,线段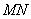 的中点为
的中点为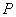 ,记直线
,记直线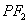 的斜率为
的斜率为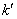 ,求证:
,求证: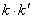 为定值.
为定值.
解证:(Ⅰ)由题意得 ,
, ,
,
所以 ,
, ,所求椭圆方程为
,所求椭圆方程为 .
.
(Ⅱ)设过点 的直线
的直线 方程为:
方程为: ,
,
设点 ,点
,点
将直线 方程
方程 代入椭圆
代入椭圆
整理得: 因为点
因为点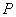 在椭圆内,所以直线
在椭圆内,所以直线 和椭圆都相交,
和椭圆都相交, 恒成立,
恒成立,
且

直线 的方程为:
的方程为: ,直线
,直线 的方程为:
的方程为:
令 ,得点
,得点 ,
, ,
,
所以点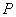 的坐标
的坐标
直线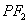 的斜率为
的斜率为

将 代入上式得:
代入上式得:

所以 为定值
为定值

练习册系列答案
相关题目
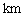 ,货车从甲地匀速
,货车从甲地匀速 行驶到乙地,速度不得超过80
行驶到乙地,速度不得超过80 ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的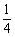 倍,固定成本为a元.
倍,固定成本为a元.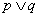 为真”是“
为真”是“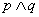 为真”的充分不必要条件;
为真”的充分不必要条件;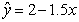 ,则变量
,则变量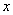 每增加一个单位,
每增加一个单位,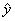 平均减少
平均减少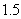 个单位;
个单位;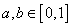 ,则不等式
,则不等式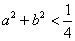 成立的概率是
成立的概率是 ;
;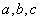 ,若
,若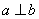 ,
,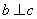 ,则
,则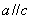 .
.  的三次幂可用奇数进行以下方式的“分裂”:
的三次幂可用奇数进行以下方式的“分裂”: .仿此,若
.仿此,若 的“分裂数”中有一个是2015,
的“分裂数”中有一个是2015, .
.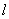 过抛物线
过抛物线 的焦点F,且和
的焦点F,且和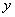 轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).
轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).  B.
B. C.
C.  D.
D. 
 的左、右焦点分别是
的左、右焦点分别是 、
、 ,其一条渐近线方程为
,其一条渐近线方程为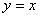 ,点
,点 在双曲线上.则
在双曲线上.则 ·
· =( ).
=( ). ,
, (
( 为虚数单位).在复平面内,
为虚数单位).在复平面内, 对应的点在第 象限.
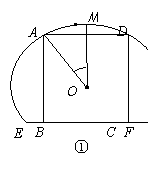
对应的点在第 象限.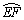 的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=
的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=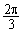 .将弓形薄铁片裁剪成尽可能大的矩形铁片ABCD(不计损耗), AD∥EF,且点A、D在
.将弓形薄铁片裁剪成尽可能大的矩形铁片ABCD(不计损耗), AD∥EF,且点A、D在 .
. 的函数关系式;
的函数关系式;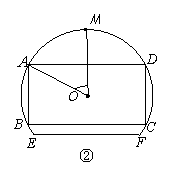 (2)当矩形铁片ABCD的
(2)当矩形铁片ABCD的 面积最大时,求cos
面积最大时,求cos