题目内容
(本题满分12分)如图所示,四棱锥P—ABCD中,AB AD,CD
AD,CD AD,PA
AD,PA 底面ABCD,PA=AD=CD=2AB=2,M为PC的中点。
底面ABCD,PA=AD=CD=2AB=2,M为PC的中点。
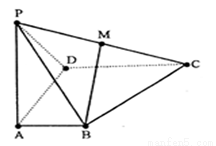
(1)求证:BM∥平面PAD;
(2)在侧面PAD内找一点N,使MN 平面PBD;
平面PBD;
(3)求直线PC与平面PBD所成角的正弦。
(1)详见解析;(2)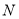 是
是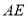 的中点;(3)
的中点;(3)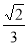 .
.
【解析】
试题分析:(1)取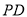 的中点
的中点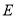 ,连接
,连接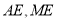 ,则可证得四边形
,则可证得四边形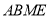 为平行四边形,可得
为平行四边形,可得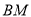 ∥
∥ ,根据线面平行的判定定理可证得
,根据线面平行的判定定理可证得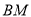 ∥
∥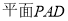 .(2)以
.(2)以 为原点,以
为原点,以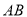 、
、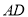 、
、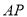 所在直线为
所在直线为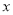 轴、
轴、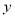 轴、
轴、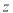 轴建立空间直角坐标系,在平面
轴建立空间直角坐标系,在平面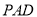 内设
内设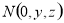 ,从而可求得各向量坐标.根据两向量垂直数量积为0可求得
,从而可求得各向量坐标.根据两向量垂直数量积为0可求得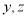 的值.(3)由(2)可知
的值.(3)由(2)可知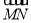 是面
是面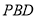 的法向量,则直线
的法向量,则直线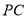 与
与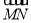 夹角的余弦值的绝对值等于直线
夹角的余弦值的绝对值等于直线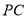 与平面
与平面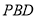 所成的角的正弦值.
所成的角的正弦值.
试题解析:(1)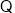
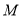 是
是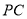 的中点,取
的中点,取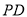 的中点
的中点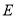 ,则
,则
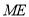

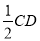 ,又
,又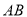

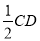
 四边形
四边形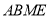 为平行四边形
为平行四边形

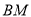 ∥
∥ ,
,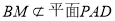
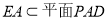

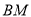 ∥
∥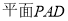 (4分)
(4分)
(2)以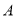 为原点,以
为原点,以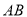 、
、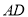 、
、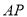 所在直线为
所在直线为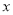 轴、
轴、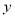 轴、
轴、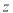 轴建立空间直角坐标系,如图,则
轴建立空间直角坐标系,如图,则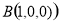 ,
,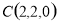 ,
,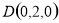 ,
,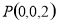 ,
, ,
,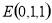
在平面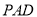 内设
内设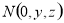 ,
,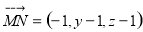 ,
, ,
,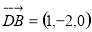 由
由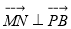

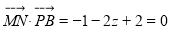


由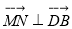

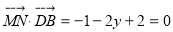

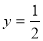

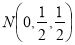

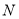 是
是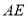 的中点,此时
的中点,此时 (8分)
(8分)
(3)设直线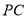 与平面
与平面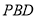 所成的角为
所成的角为
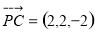 ,
,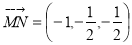 ,设
,设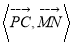 为
为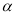
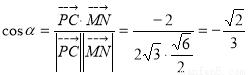
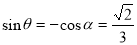
故直线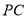 与平面
与平面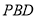 所成角的正弦为
所成角的正弦为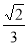 (12分)
(12分)
考点:1线面平行;2用空间向量解决立体几何问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有公共焦点,且离心率
有公共焦点,且离心率 的双曲线方程为( )
的双曲线方程为( ) B.
B. C.
C. D.
D.
 ,所在圆的半径为10cm,则扇形的面积为___________.
,所在圆的半径为10cm,则扇形的面积为___________. 满足约束条件
满足约束条件 ,则
,则 的最大值为( )
的最大值为( ) 中,
中, 分别是角A,B,C的对边,若
分别是角A,B,C的对边,若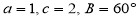 ,则
,则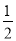 B.
B.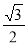 C.1 D.
C.1 D.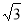
 满足
满足 ,则
,则 的最大值___________;
的最大值___________; 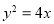 的焦点为
的焦点为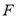 ,准线为
,准线为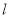 ,经过
,经过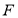 且斜率为
且斜率为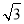 的直线与抛物线在
的直线与抛物线在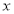 轴上方的部分相交于点
轴上方的部分相交于点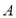 ,
,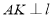 ,垂足为
,垂足为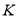 ,则
,则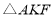 的面积是( )
的面积是( )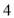 B.
B.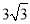 C.
C.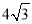 D.8
D.8 γ=m,β
γ=m,β γ=n,m∥n ,则α∥β;
γ=n,m∥n ,则α∥β;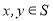 ,都有
,都有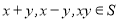 ,则称S为封闭集。下列命题:
,则称S为封闭集。下列命题: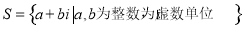 为封闭集;
为封闭集;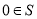 ;
;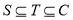 的任意集合
的任意集合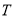 也是封闭集.
也是封闭集.