Question

已知长方体的一条对角线与长方体的两条棱所成角为45°和60°，且体积为4，求长方体的表面积．

Answer 1

考点：棱柱、棱锥、棱台的侧面积和表面积

专题：空间位置关系与距离

分析：对角线BD₁=a，由已知可以用a表示长方体的长、宽、高，代入体积公式，可能求出a值，进而求出长方体的长、宽、高，进而得到答案．

解答： 解：如图所示：在长方体BD₁中，对角线BD₁与棱DD₁的夹角为45°，与AB的夹角为60°，

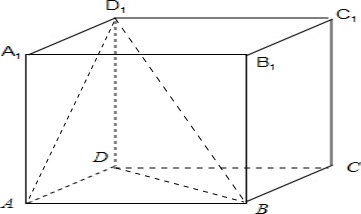
设对角线BD₁=a，则BD=DD₁=

2

2

a，AB=

1

2

a，AD₁=

3

2

a，
则AD=

1

2

a，
则长方体BD₁的体积V=AD•AB•DD₁=

2

8

a3=4
解得a=2

2

，
∴DD₁=2，AB=AD=

2

，
故长方体的表面积S=2×(

2

)2+4×2×

2

=4+8

2

点评：本题考查的知识点是棱柱的体积和表面积，求出长方体的长、宽、高，是解答的关键．