题目内容
8.已知函数f(x)=$\frac{x^2-ax+a}{x}$,x∈[1,+∞).(1)当a=4时,求函数f(x)的最小值;
(2)若对任意x∈(2,+∞),f(x)>0恒成立,试求实数a的取值范围.
分析 (1)利用基本不等式的性质进行求解即可.
(2)利用参数分离法结合基本不等式的性质进行求解.
解答 解:(1)当a=4时,f(x)=$\frac{x^2-ax+a}{x}$=$\frac{{x}^{2}-4x+4}{x}$=x+$\frac{4}{x}$-4,
∵x≥1,∴f(x)=x+$\frac{4}{x}$-4≥2$\sqrt{x•\frac{4}{x}}$-4=4-4=0,
当且仅当x=$\frac{4}{x}$,即x=2时取等号,
即函数f(x)的最小值为0
(2)若对任意x∈(2,+∞),f(x)>0恒成立,
即若对任意x∈(2,+∞),$\frac{x^2-ax+a}{x}$>0恒成立,
即x2-ax+a>0,
即x2>a(x-1),
即a<$\frac{{x}^{2}}{x-1}$,
设h(x)=$\frac{{x}^{2}}{x-1}$,则h(x)=$\frac{{x}^{2}}{x-1}$=$\frac{(x-1)^{2}+2(x-1)+1}{x-1}$=(x-1)+$\frac{1}{x-1}$+2,
∵x>2,
∴x-1>1,
设t=x-1,则t>1,
则函数g(t)=t+$\frac{1}{t}$+2在(1,+∞)上为增函数,
则g(t)>g(1)=1+1+2=4,
∴a≤4.
点评 本题主要考查不等式恒成立问题,利用参数分离法以及构造法结合基本不等式的性质是解决本题的关键.综合性较强.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
18.设函数f(x)=|2x-1|,c<b<a,且f(c)>f(a)>f(b),则2a+2c与2的大小关系是( )
| A. | 2a+2c>2 | B. | 2a+2c≥2 | C. | 2a+2c≤2 | D. | 2a+2c<2 |
3.函数f(x)的导函数f′(x)的图象如图所示,则函数f(x)的解析式可能为( )
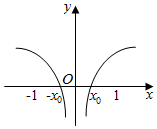

| A. | $\frac{{e}^{x}}{x}$ | B. | x2•lnx | C. | $\frac{{e}^{|x|}}{x}$ | D. | x•lnx2 |
13.某工厂甲乙两名工人参加操作技能培训,他们在培训期间参加的8次测试成绩记录如下:
(1)用茎叶图表示甲乙两人的成绩;
(2)请根据茎叶图分析甲乙两人的成绩.
| 甲 | 95 | 82 | 88 | 81 | 93 | 79 | 84 | 78 |
| 乙 | 83 | 92 | 80 | 95 | 90 | 80 | 85 | 75 |
(2)请根据茎叶图分析甲乙两人的成绩.
17.已知f(x)=sinnx,则f′(x)=( )
| A. | nsinn-1x | B. | ncosn-1x | C. | cosnx | D. | nsinn-1x•cosx |