题目内容
1.设函数f(x)=$\left\{\begin{array}{l}{ax+b,x<0}\\{{2}^{x},x≥0}\end{array}\right.$,且f(-2)=3,f(-1)=f(1).( I)求f(x)的解析式;
( II)画出f(x)的图象(不写过程)并求其值域.
分析 ( I)根据定义域的范围带值计算求出a,b即可得f(x)的解析式.
( II)根据一次函数和指数函数的性质画图象,通过图象得结论.
解答 解:( I)函数f(x)=$\left\{\begin{array}{l}{ax+b,x<0}\\{{2}^{x},x≥0}\end{array}\right.$,
由f(-2)=3,f(-1)=f(1).
则有$\left\{\begin{array}{l}{-2a+b=3}\\{-a+3=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=1}\end{array}\right.$
则f(x)=$\left\{\begin{array}{l}{-x+1,x<0}\\{{2}^{x},x≥0}\end{array}\right.$,
(Ⅱ)f(x)的图象如图: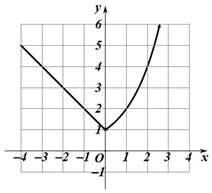
通过函数f(x)的图象可知值域为[1,+∞).
点评 本题考查了分段函数的解析式的求法和函数的画法.通过图象读性质.属于基础题.

练习册系列答案
相关题目
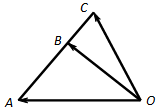
12.如图,$\overrightarrow{AB}$=2$\overrightarrow{BC},\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列等式中成立的是( )

| A. | $\overrightarrow{c}$=3$\overrightarrow{a}$-$\overrightarrow{b}$ | B. | $\overrightarrow{c}$=3$\overrightarrow{b}$-$\overrightarrow{a}$ | C. | $\overrightarrow{c}$=$\frac{3}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$ | D. | $\overrightarrow{c}$=$\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ |
9.已知奇函数f(x)在区间[1,6]是增函数,且最大值为10,最小值为4,则其在[-6,-1]上的最大值、最小值分别是( )
| A. | -4,-10 | B. | 4,-10 | C. | 10,4 | D. | 不确定 |
6.已知等差数列{an}的前项和为Sn,若$\overrightarrow{OB}$=a1005O$\overrightarrow{OA}$+a1006$\overrightarrow{OC}$,且A、B、C三点共线(该直线不经过坐标原点O),则S2010=( )
| A. | 1005 | B. | 1010 | C. | 2009 | D. | 2010 |
9.已知函数f(x)的定义域为(0,+∞),且满足f(x)+x•f'(x)>0(f'(x)是f(x)的导函数),则不等式(x-1)f(x2-1)<f(x+1)的解集为( )
| A. | (-1,2) | B. | (1,2) | C. | (1,+∞) | D. | (-∞,2) |