题目内容
(本小题满分14分)已知圆 的圆心坐标为
的圆心坐标为 , 直线
, 直线 与圆
与圆 相交于
相交于 、
、 两点,
两点,
 .
.
(1)求圆 的方程;
的方程;
(2)若 , 过点
, 过点 作圆
作圆 的切线, 切点为
的切线, 切点为 ,记
,记
 , 点
, 点 到直线
到直线 的距离为
的距离为 , 求
, 求 的取值范围.
的取值范围.
(1)圆 的方程为
的方程为 ;(2)
;(2) 的取值范围是
的取值范围是 .
.
【解析】
试题分析:根据点到直线的距离公式先算出圆心 到直线
到直线 距离
距离 ,进行根据所给的弦长
,进行根据所给的弦长 ,可由公式
,可由公式 ,求出圆
,求出圆 的半径
的半径 ,进而可写出圆的标准方程;(1)根据(1)中圆
,进而可写出圆的标准方程;(1)根据(1)中圆 的圆心及半径,结合切线长公式
的圆心及半径,结合切线长公式
 算出
算出 ,再根据点到直线的距离公式算出
,再根据点到直线的距离公式算出
 ,进而得出
,进而得出
 ,令
,令 ,将其转化成
,将其转化成
 ,结合
,结合 的范围,根据函数的性质即可确定
的范围,根据函数的性质即可确定 的取值范围.
的取值范围.
试题解析:(1)设圆 的半径为
的半径为 ,圆
,圆 的圆心
的圆心 到直线
到直线 的距离
的距离 2分
2分
∵
 ,∴
,∴ 3分
3分
∴ 4分
4分
解得 5分
5分
∴所求的圆 的方程为
的方程为 6分
6分
(2)∵圆 :
: 的圆心
的圆心 ,半径
,半径
∴




 8分
8分
又点 到直线
到直线 的距离
的距离
 9分
9分
∴
 10分
10分
令 ,则
,则 11分
11分
∵ ,∴
,∴
∴


 12分
12分
∵ ,∴
,∴ ,∴
,∴
∴ 13分
13分
∴


∴ 的取值范围是
的取值范围是 14分.
14分.
考点:1.点到直线的距离公式;2.圆的标准方程;2.直线与圆的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 及对应的一个特征向量
及对应的一个特征向量 和特征值
和特征值 及对应的一个特征向量
及对应的一个特征向量 ,试求矩阵A.
,试求矩阵A. ,则目标函数
,则目标函数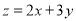 的最小值为( )
的最小值为( )
 的左焦点为F,若F关于直线
的左焦点为F,若F关于直线 的对称点A是椭圆C上的点,则椭圆C的离心率为( )
的对称点A是椭圆C上的点,则椭圆C的离心率为( ) B.
B. C.
C. D.
D.
 ,则目标函数
,则目标函数 的最小值为( )
的最小值为( ) 且
且 的图象恒过点
的图象恒过点 . 若点
. 若点 上, 则
上, 则 的最小值为 .
的最小值为 . 、
、 满足条件
满足条件 则
则 的最大值为( )
的最大值为( ) B.
B. C.
C. D.
D.
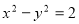 绕原点逆时针转动
绕原点逆时针转动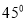 ,就会得到它的一条“任性双曲线”
,就会得到它的一条“任性双曲线”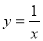 ;根据以上材料可推理得出双曲线
;根据以上材料可推理得出双曲线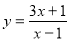 的焦距为( )
的焦距为( )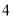 B.
B. 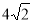 C.
C. 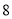 D.
D. 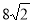
 分别是与
分别是与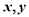 轴正方向同向的单位向量,平面内三点
轴正方向同向的单位向量,平面内三点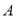 、
、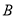 、
、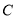 满足
满足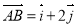 ,
, ,
,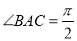 ,则实数m的值为 .
,则实数m的值为 .