题目内容
如图2-1-4,在△ABC中,E、F为AB、AC中点,G、H为AE、AF中点.求证:BC=4GH.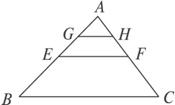
图2-1-4
思路分析:此题可利用三段论来证明,分清大前提与小前提是解决问题的关键.
证明:因为连结三角形两边中点的线段是三角形中位线(大前提),
又∵在△ABC中,E、F分别为AB、AC的中点(小前提),
∴EF为△ABC中位线(结论).
同理,GH为△AEF中位线.
因为三角形中位线平行于第三边且等于第三边的一半(大前提),
又∵EF为△ABC中位线(小前提),
∴EF=
BC(结论).
同理,GH=
EF.
∴GH=
EF=
BC,即BC=4GH.
练习册系列答案
相关题目
=
,在
上任取一点P,PB、PC与AD的交点分别为E、F,则图中相似三角形的组数是( )
