Question

【题目】如图，,是经过小城的东西方向与南北方向的两条公路，小城位于小城的东北方向，直线距离.现规划经过小城修建公路(,分别在与上)，与,围成三角形区域.

(1)设，,求三角形区域周长的函数解析式;

(2)现计划开发周长最短的三角形区域，求该开发区域的面积.

Answer 1

【答案】（1）

（2）开发区域的面积为

【解析】分析：(1)先根据直角三角形求OA,OB,AB，再相加得三角形区域周长的函数解析式; (2) 令，化简，再根据三角函数有界性确定t范围，解得最小值，同时求出开发区域的面积.

详解：解：（方法一）

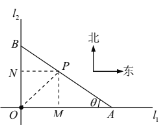
（1）如图，过分别作、的垂线，垂足分别为、，因为小城位于小城的东北方向，且，所以，在和中，易得，

，

所以

当时，，单调递减

当时，，单调递增

所以时，取得最小值.

此时，，

的面积

答：开发区域的面积为

（方法二）

（1）在中，，即

所以

在中，

所以

（2）令，则

因为，所以，所以

由 ，得

记

因为在上单调递减，所以当时最小

此时，即

，

所以的面积

答：开发区域的面积为