题目内容
(本小题满分12分)
如图,已知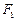 ,
,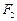 分别是椭圆
分别是椭圆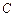 :
: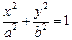 (
(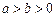 )的左、右焦点,且椭圆
)的左、右焦点,且椭圆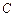 的离心率
的离心率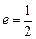 ,
,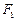 也是抛物线
也是抛物线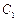 :
: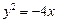 的焦点.
的焦点.
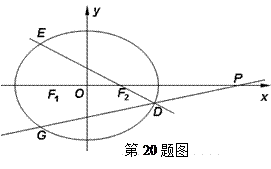
(Ⅰ)求椭圆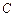 的方程;
的方程;
(Ⅱ)过点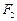 的直线
的直线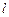 交椭圆
交椭圆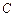 于
于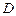 ,
,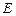 两点,且
两点,且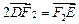 ,点
,点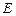 关于
关于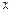 轴的对称点为
轴的对称点为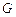 ,求直线
,求直线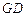 的方程.
的方程.
如图,已知
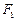 ,
,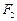 分别是椭圆
分别是椭圆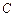 :
: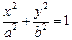 (
(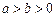 )的左、右焦点,且椭圆
)的左、右焦点,且椭圆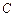 的离心率
的离心率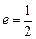 ,
,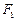 也是抛物线
也是抛物线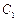 :
: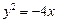 的焦点.
的焦点.
(Ⅰ)求椭圆
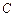 的方程;
的方程;(Ⅱ)过点
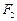 的直线
的直线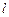 交椭圆
交椭圆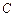 于
于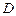 ,
,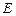 两点,且
两点,且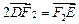 ,点
,点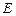 关于
关于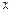 轴的对称点为
轴的对称点为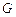 ,求直线
,求直线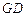 的方程.
的方程.解:(Ⅰ)因为抛物线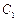 的焦点是
的焦点是 ,
,
则 ,得
,得 ,则
,则 ,
,
故椭圆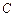 的方程为
的方程为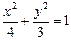 .
.
(Ⅱ)显然直线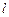 的斜率不存在时不符合题意,可设直线
的斜率不存在时不符合题意,可设直线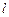 :
: ,设
,设 ,
, ,由于
,由于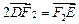 ,
,
则 ,联立
,联立 ,
, ,
,
则 ,……
,…… ①
①  ,……②,
,……②, 代入①、②得,
代入①、②得,
 ,……③
,……③  ,……④ 由③、④得
,……④ 由③、④得 ,
,

 ,
, ,
,
(i)若 时,
时, ,
,
 ,
,
即 ,
, ,
,
 ,
,
直线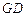 的方程是
的方程是 ;
;
(ii)当 时,同理可求直线
时,同理可求直线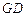 的方程是
的方程是 .
.
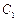 的焦点是
的焦点是 ,
,则
 ,得
,得 ,则
,则 ,
,故椭圆
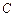 的方程为
的方程为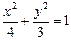 .
.(Ⅱ)显然直线
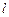 的斜率不存在时不符合题意,可设直线
的斜率不存在时不符合题意,可设直线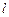 :
: ,设
,设 ,
, ,由于
,由于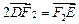 ,
,则
 ,联立
,联立 ,
, ,
,则
 ,……
,…… ①
①  ,……②,
,……②, 代入①、②得,
代入①、②得, ,……③
,……③  ,……④ 由③、④得
,……④ 由③、④得 ,
,
 ,
, ,
,(i)若
 时,
时, ,
,
 ,
,即
 ,
, ,
,
 ,
,直线
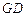 的方程是
的方程是 ;
;(ii)当
 时,同理可求直线
时,同理可求直线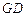 的方程是
的方程是 .
.略

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 1,y1),C(x2,y2)满足条件|F2A|,|F2B|,|F2C|成等差数列.(1)求该椭圆的方程;(2)求弦AC中点的横坐标.
1,y1),C(x2,y2)满足条件|F2A|,|F2B|,|F2C|成等差数列.(1)求该椭圆的方程;(2)求弦AC中点的横坐标. 中,已知椭圆
中,已知椭圆 .如图所示,斜率为
.如图所示,斜率为 且不过原点的直线
且不过原点的直线 交椭圆
交椭圆 于
于 ,
, 两点,线段
两点,线段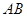 的中点为
的中点为 ,射线
,射线 交椭圆
交椭圆 ,交直线
,交直线 于点
于点 .
. 的最小值;
的最小值;
 ?
? ,(i)求证:直线
,(i)求证:直线 轴对称?若能,求出此时
轴对称?若能,求出此时 的外接圆方程;若不能,请说明理由.
的外接圆方程;若不能,请说明理由. 的离心率为
的离心率为 ,且两个焦点和短轴的一个端点是一个等腰三角形的顶点.斜率为
,且两个焦点和短轴的一个端点是一个等腰三角形的顶点.斜率为 的直线
的直线 过椭圆的上焦点且与椭圆相交于
过椭圆的上焦点且与椭圆相交于 ,
, 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与 轴相交于点
轴相交于点 .
. 的取值范围;
的取值范围; 的面积,并求面积的最大值.
的面积,并求面积的最大值.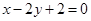 经过椭圆
经过椭圆 的一个焦点和一个顶点,则该椭圆的离心率为
的一个焦点和一个顶点,则该椭圆的离心率为



 上的动点,F1、F2分别为左、右焦点,O为坐标原点,则
上的动点,F1、F2分别为左、右焦点,O为坐标原点,则 的取值范围是
的取值范围是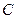 的两焦点为
的两焦点为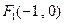 ,
,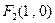 ,并且经过点
,并且经过点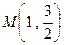 .
.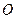 :
: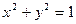 ,直线
,直线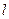 :
: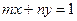 ,证明当点
,证明当点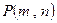 在椭圆
在椭圆 ,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于
,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于 点Q,则点Q(x,y)所满足的轨迹方程为 ( ▲ )
点Q,则点Q(x,y)所满足的轨迹方程为 ( ▲ )



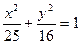 的焦点为F1,F
的焦点为F1,F 2,P为椭圆上一点,若
2,P为椭圆上一点,若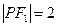 ,则
,则