题目内容
定义在R上的函数f(x)满足:
(1)f(x)+f(y)+1≥f(x+y)≥f(x)+f(y);
(2)f(0)≥f(x),x∈[0,1);
(3)-f(-1)=f(1)=1
(Ⅰ)求f(0);
(Ⅱ)当x∈[0,1)时,求证:f(x)=0
(Ⅲ)若集合M={(x,y)|f(x)f(y)=7},求集合M在平面直角坐标系中对应的平面区域的面积.
(1)f(x)+f(y)+1≥f(x+y)≥f(x)+f(y);
(2)f(0)≥f(x),x∈[0,1);
(3)-f(-1)=f(1)=1
(Ⅰ)求f(0);
(Ⅱ)当x∈[0,1)时,求证:f(x)=0
(Ⅲ)若集合M={(x,y)|f(x)f(y)=7},求集合M在平面直角坐标系中对应的平面区域的面积.
考点:抽象函数及其应用
专题:计算题,证明题,函数的性质及应用
分析:(Ⅰ)令x=y=0,得f(0)≤0,再令x=1,y=-1,得f(0)≥0,即f(0)=0;
(Ⅱ)运用反证法,假设?x0∈[0,1),使得f(x0)<0,由条件推出矛盾即可;
(Ⅲ)由条件推得f(x+1)=f(x)+1,再由累加法得到f(x+n)=f(x)+n,又由f(x)=0,x∈[0,1),因为7为素数,故f(x)f(y)=1×7,得到四种情况,分别求出x,y的范围,计算面积,求和即可.
(Ⅱ)运用反证法,假设?x0∈[0,1),使得f(x0)<0,由条件推出矛盾即可;
(Ⅲ)由条件推得f(x+1)=f(x)+1,再由累加法得到f(x+n)=f(x)+n,又由f(x)=0,x∈[0,1),因为7为素数,故f(x)f(y)=1×7,得到四种情况,分别求出x,y的范围,计算面积,求和即可.
解答:
(Ⅰ)解:令x=y=0,得f(0)≥2f(0),即f(0)≤0
再令x=1,y=-1,得f(0)≥f(1)+f(-1)=0,故f(0)=0.
(Ⅱ)证明:假设?x0∈[0,1),使得f(x0)<0,则f(1-x0)<0,由已知可得:
f(x0)+f(1-x0)+1≥f(1)=1,即f(x0)+f(1-x0)≥0,与假设矛盾,得证.
(Ⅲ)解:由已知:f(x+1)≥f(x)+f(1)=f(x)+1,f(x)≥f(x+1)+f(-1)=f(x+1)-1
即f(x+1)≤f(x)+1,所以f(x+1)=f(x)+1
所以f(x+1)-f(x)=1,f(x+2)-f(x+1)=1,…,f(x+n)-f(x+n-1)=1相加得:f(x+n)=f(x)+n
又由f(x)=0,x∈[0,1),可知f(x)在R上不减,
且x>0时,都有f(x)≥0,x<0时,都有f(x)≤0,
又因为7为素数,故f(x)f(y)=1×7,所以:
或
或
或
可得:
或
或
或
它们分别代表四个边长为1的正方形,故面积和为4.
即集合M在平面直角坐标系中对应的平面区域的面积为4.
再令x=1,y=-1,得f(0)≥f(1)+f(-1)=0,故f(0)=0.
(Ⅱ)证明:假设?x0∈[0,1),使得f(x0)<0,则f(1-x0)<0,由已知可得:
f(x0)+f(1-x0)+1≥f(1)=1,即f(x0)+f(1-x0)≥0,与假设矛盾,得证.
(Ⅲ)解:由已知:f(x+1)≥f(x)+f(1)=f(x)+1,f(x)≥f(x+1)+f(-1)=f(x+1)-1
即f(x+1)≤f(x)+1,所以f(x+1)=f(x)+1
所以f(x+1)-f(x)=1,f(x+2)-f(x+1)=1,…,f(x+n)-f(x+n-1)=1相加得:f(x+n)=f(x)+n
又由f(x)=0,x∈[0,1),可知f(x)在R上不减,
且x>0时,都有f(x)≥0,x<0时,都有f(x)≤0,
又因为7为素数,故f(x)f(y)=1×7,所以:
|
|
|
|
可得:
|
|
|
|
它们分别代表四个边长为1的正方形,故面积和为4.
即集合M在平面直角坐标系中对应的平面区域的面积为4.
点评:本题考查抽象函数及应用,考查两边夹法则的运用,以及反证法,以及累加法求函数解析式,是一道综合题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题: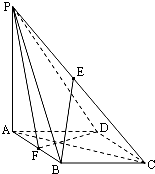 如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB中点.
如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB中点.