题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}\frac{2}{x},x≥2\\{(x-1)^3},0<x<2\end{array}\right.$,若关于x的方程f(x)=kx有两个不同的实根,则实数k的取值范围是( )| A. | $({0,\frac{1}{2}})$ | B. | $({0,\frac{{\sqrt{2}}}{4}})∪({\frac{{\sqrt{2}}}{4},\frac{1}{2}})$ | C. | $({\frac{{\sqrt{2}}}{4},+∞})$ | D. | $[{\frac{1}{2},2\sqrt{2}}]$ |
分析 由题意可得函数f(x)的图象和直线y=kx有2个交点,数形结合可得当直线的斜率k的范围.
解答 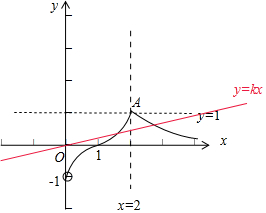 解:画出函数f(x)和y=kx的图象,如图,点A(2,1),
解:画出函数f(x)和y=kx的图象,如图,点A(2,1),
由题意可得函数f(x)的图象和直线y=kx有2个交点,
数形结合可得当直线的斜率k满足0<k<$\frac{1}{2}$时,
函数f(x)的图象和直线y=kx有2个交点,
故选:A.
点评 本题主要考查函数零点与方程的根的关系,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
15.实数X,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+3y-3≥0\\ 3x+y-9≤0\end{array}\right.$,若z=ax+y的最大值为2a+3,则a的取值范围是( )
| A. | [-3,1] | B. | [-1,3] | C. | (-∞,1] | D. | [3,+∞) |
13.已知函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x},}&{0<x≤3}\\{-\frac{2}{3}x+\frac{16}{3},}&{x>3}\end{array}\right.$,若函数g(x)=f(x)-m有三个互不相等的零点a、b、c,则abc的取值范围为( )
| A. | (2,$\frac{10}{3}$) | B. | (0,5) | C. | (6,10) | D. | (3,5) |
20.若复数1-$\sqrt{3}i$(i为虚数单位),是z的共轭复数,则在复平面内,复数z对应的点的坐标为( )
| A. | (0,1) | B. | (1,-$\sqrt{3}$) | C. | (-1,-$\sqrt{3}$) | D. | (-1,0) |
17.设变量x、y满足约束条件$\left\{\begin{array}{l}x+y≤3\\ x-y≥-1\\ y≥1\end{array}\right.$,则目标函数z=-2x+y的最大值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
15.在各项均为正数的等比数列{an}中,已知a1a5=25,则a3等于( )
| A. | 5 | B. | 25 | C. | -25 | D. | -5或5 |