题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x},}&{0<x≤3}\\{-\frac{2}{3}x+\frac{16}{3},}&{x>3}\end{array}\right.$,若函数g(x)=f(x)-m有三个互不相等的零点a、b、c,则abc的取值范围为( )| A. | (2,$\frac{10}{3}$) | B. | (0,5) | C. | (6,10) | D. | (3,5) |
分析 先画出分段函数的图象,根据图象确定字母a、b、c的取值范围,最后数形结合写出其取值范围即可
解答 解:由g(x)=f(x)-m=0得m=f(x),
若函数g(x)=f(x)-m有三个互不相等的零点a、b、c,
即等价为函数y=f(x)与y=m有三个互不相同的交点,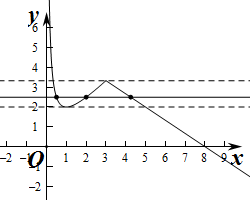
作出函数f(x)的图象如图:
当x>3时,f(x)=$-\frac{2}{3}x+\frac{16}{3}$≤$-\frac{2}{3}×3+\frac{16}{3}$=$\frac{10}{3}$,
∵函数f(x)=x+$\frac{1}{x}$在(0,1]上递减,在[1,3]上递增,
∴2≤f(x)≤$\frac{10}{3}$,
∴若函数y=f(x)与y=m有三个互不相同的交点,
则2<m<$\frac{10}{3}$,
设a<b<c,
由f(x)=x+$\frac{1}{x}$=$\frac{10}{3}$,
解得x=$\frac{1}{3}$或x=3,
由f(x)=$-\frac{2}{3}x+\frac{16}{3}$=2,解得x=5,
则$\frac{1}{3}$<a<1,1<b<3,3<c<5,
当0<x≤3时,由g(x)=f(x)-m=x+$\frac{1}{x}$-m=$\frac{{x}^{2}-mx+1}{x}$=0得x2-mx+1=0,
则ab=1,
故abc=c,
即abc的范围就是c的范围是(3,5),
故选:D
点评 本题考查了分段函数图象的画法及其应用,对数函数及一次函数图象的画法,数形结合求参数的取值范围,画出分段函数图象并数形结合解决问题是解决本题的关键.

练习册系列答案
相关题目
4.已知角α终边与单位圆x2+y2=1的交点为$P(\frac{1}{2},y)$,则$sin(\frac{π}{2}+2α)$=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 1 |
1.函数f(x)=sin(-2x)的一个递增区间是( )
| A. | $(0,\frac{π}{4})$ | B. | $(-π,-\frac{π}{2})$ | C. | $(\frac{3π}{4},2π)$ | D. | $(-\frac{π}{2},-\frac{π}{4})$ |
18.三棱锥P-ABC中,已知∠APC=∠BPC=∠APB=$\frac{π}{3}$,点M是△ABC的重心,且$\overrightarrow{PA}$•$\overrightarrow{PB}$+$\overrightarrow{PB}$$•\overrightarrow{PC}$+$\overrightarrow{PC}$$•\overrightarrow{PA}$=9,则|$\overrightarrow{PM}$|的最小值为( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{6}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2 |
5.已知函数f(x)=$\left\{\begin{array}{l}\frac{2}{x},x≥2\\{(x-1)^3},0<x<2\end{array}\right.$,若关于x的方程f(x)=kx有两个不同的实根,则实数k的取值范围是( )
| A. | $({0,\frac{1}{2}})$ | B. | $({0,\frac{{\sqrt{2}}}{4}})∪({\frac{{\sqrt{2}}}{4},\frac{1}{2}})$ | C. | $({\frac{{\sqrt{2}}}{4},+∞})$ | D. | $[{\frac{1}{2},2\sqrt{2}}]$ |