题目内容
已知函数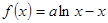 .
.
(1)当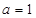 时,求
时,求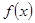 的极值;
的极值;
(2)若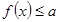 对
对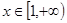 恒成立,求实数
恒成立,求实数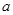 的取值范围.
的取值范围.
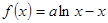 .
.(1)当
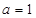 时,求
时,求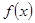 的极值;
的极值;(2)若
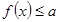 对
对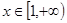 恒成立,求实数
恒成立,求实数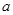 的取值范围.
的取值范围.(1) (2)
(2) 
 (2)
(2) 
试题分析:
(1)确定定义域,保证函数有意义;求导函数,令其等于0,得
 ,判断其单调性,从而确定其极值.
,判断其单调性,从而确定其极值.(2)根据
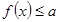 对
对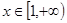 恒成立,可知函数
恒成立,可知函数 在
在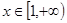 上的最大值小于等于
上的最大值小于等于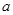 恒成立.利用导数, 通过讨论
恒成立.利用导数, 通过讨论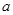 的范围,判断函数的单调性,从而找到函数的最值,最终确定
的范围,判断函数的单调性,从而找到函数的最值,最终确定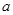 的范围.
的范围.(1)函数的定义域为
 ,由
,由 ,知
,知 .
.令
 ,得
,得 .显然
.显然
 .
.当
 时,
时,
 是增函数;
是增函数;当
 时,
时,
 是减函数.
是减函数. 的极大值
的极大值 .
.(2)
 ,
,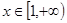
①当
 时,
时,
 是减函数,即
是减函数,即
 ;
;②当
 时,当
时,当 时,
时,
 是增函数;
是增函数;当
 时,
时,
 是减函数.
是减函数.(ⅰ)当
 时, 在
时, 在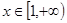 时
时 是减函数,即
是减函数,即
 ;
;(ⅱ) 当
 时,当
时,当 时,
时,
 是增函数;当
是增函数;当 时,
时,
 是减函数.
是减函数. 即
即
 .综上
.综上 .
.
练习册系列答案
相关题目
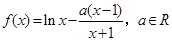 .
.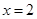 是函数
是函数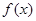 的极值点,求曲线
的极值点,求曲线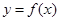 在点
在点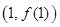 处的切线方程;
处的切线方程;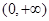 上为单调增函数,求
上为单调增函数,求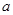 的取值范围;
的取值范围;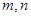 为正实数,且
为正实数,且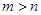 ,求证:
,求证: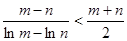 .
. 的定义域为
的定义域为 ,部分对应值如下表,
,部分对应值如下表, 的导函数
的导函数 的图像如图所示.下列命题中,真命题的个数为 ( ).
的图像如图所示.下列命题中,真命题的个数为 ( ). 第12题图
第12题图 
 是周期函数;② 函数
是周期函数;② 函数 是减函数;③ 如果当
是减函数;③ 如果当 时,
时, ,那么
,那么 的最大值为
的最大值为 ;④ 当
;④ 当 时,函数
时,函数 有
有 个
个 个
个