题目内容

1．设变量x、y满足约束条件$\left\{\begin{array}{l}{x+y≥3}\\{x-y≥-1}\\{2x-y≤3}\end{array}\right.$，则目标函数z=x2+y2的最大值为（　　）
A．9B．36C．81D．41

分析 作出可行域，z=x2+y2表示可行域内的点到原点距离的平方，数形结合可得．

解答 解：作出约束条件$\left\{\begin{array}{l}{x+y≥3}\\{x-y≥-1}\\{2x-y≤3}\end{array}\right.$，所对应的可行域，
而z=x2+y2表示可行域内的点P到原点距离的平方，
由：$\left\{\begin{array}{l}{x-y=-1}\\{2x-y=3}\end{array}\right.$，解得P（4，5）
数形结合可得最大值为：42+52=41，
故选：D．

点评 本题考查简单线性规划，准确作图是解决问题的关键，属中档题．

练习册系列答案
相关题目
11．已知函数f（x）=|2x-a|+a．
（1）当a=3时，求不等式f（x）≤6的解集；
（2）设函数g（x）=|2x-3|，?x∈R，f（x）+g（x）≥5，求a的取值范围．
12．团购已成为时下商家和顾客均非常青睐的一种省钱、高效的消费方式，不少商家同时加入多家团购网，现恰有三个团购网站在A市开展了团购业务，A市某调查公司为调查这三家团购网站在本市的开展情况，从本市已加入了团购网站的商家中随机地抽取了50家进行调查，他们加入这三家团购网站的情况如下图所示．
（Ⅰ）从所调查的50家商家中任选两家，求他们加入团购网站的数量不相等的概率；
（Ⅱ）从所调查的50家商家中任选两家，用ξ表示这两家商家参加的团购网站数量之差的绝对值，求随机变量ξ的分布列和数学期望；
（Ⅲ）将频率视为概率，现从A市随机抽取3家已加入团购网站的商家，记其中恰好加入了两个团购网站的商家数为η，试求事件“η≥2”的概率．
9．已知函数f（x）=lnx-2ax，a∈R．
（Ⅰ）若函数y=f（x）存在与直线2x-y=0垂直的切线，求实数a的取值范围；
（Ⅱ）设g（x）=f（x）+$\frac{1}{2}{x^2}$，若g（x）有极大值点x1，求证：$\frac{{ln{x_1}}}{x_1}+\frac{1}{{{x_1}^2}}$＞a．
16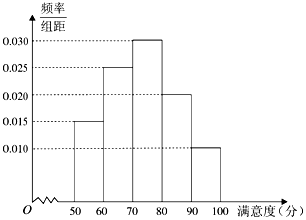．某校学生营养餐由A和B两家配餐公司配送．学校为了解学生对这两家配餐公司的满意度，采用问卷的形式，随机抽取了40名学生对两家公司分别评分．根据收集的80份问卷的评分，得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表：
满意度
评分分组		频数
[50，60）2
[60，70）8
[70，80）14
[80，90）14
[90，100]2
（Ⅰ）根据A公司的频率分布直方图，估计该公司满意度评分的中位数；
（Ⅱ）从满意度高于90分的问卷中随机抽取两份，求这两份问卷都是给A公司评分的概率；
（Ⅲ）请从统计角度，对A、B两家公司做出评价．
6．设实数x、y满足$\left\{\begin{array}{l}{2x+y≥4}\\{x-y≥-1}\\{x-2y≤2}\end{array}\right.$，则z=x+y为（　　）
A．有最小值2，无最大值B．有最小值2，最大值3
C．有最大值3，无最小值D．既无最小值，也无最大值
4．f（x）=$\frac{{x}^{{n}^{2}}}{{x}^{3n}}$（n∈Z）是偶函数，且y=f（x）在（0，+∞）上是减函数，则n=1或2．
1．已知圆O：x2+y2=1和定点A（2，1），由圆外一点P（a，b）向圆O引切线PQ，切点为Q，且满足|PQ|=|PA|．
（1）求实数a，b间满足的等量关系式；
（2）求△OQP面积的最小值；
（3）求||PO|-|PA||的最大值．
2．设正数x，y满足log${\;}_{\frac{1}{3}}$x+log3y=m（m∈[-1，1]），若不等式3ax2-18xy+（2a+3）y2≥（x-y）2有解，则实数a的取值范围是（　　）
A．（1，$\frac{55}{29}$]B．（1，$\frac{31}{21}$]C．[$\frac{31}{21}$，+∞）D．[$\frac{55}{29}$，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网