题目内容
已知z1=2+i,
=1-i,在复平面内复数
所对应的点位于第 象限.
. |
| z2 |
| z1 |
| z2 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:把复数除法运算法则,化简为a+bi(a、b∈R)的形式,可以判断所在象限.
解答:
解:∵z1=2+i,
=1-i,则
=
=
=
,
∴在复平面内复数
所对应的点(
,-
)位于第二象限.
故答案为:二.
. |
| z2 |
| z1 |
| z2 |
| 2+i |
| 1+i |
| (2+i)(1-i) |
| (1+i)(1-i) |
| 1-i |
| 2 |
∴在复平面内复数
| z1 |
| z2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:二.
点评:本题考查复数代数形式的运算,复数和复平面内点的对应关系,是基础题.

练习册系列答案
相关题目
函数f(x)=cosπx-|log2|x-1||的所有零点之和为( )
| A、6 | B、4 | C、2 | D、0 |
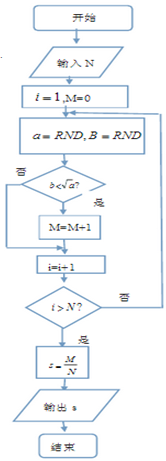 在程序中,x=RND表示将计算机产生的[0,1]区间上的均匀随机数赋给变量x.利用如图的程序框图进行随机模拟,我们发现:随着输入N值的增加,输出的S值稳定在某个常数上.这个常数是
在程序中,x=RND表示将计算机产生的[0,1]区间上的均匀随机数赋给变量x.利用如图的程序框图进行随机模拟,我们发现:随着输入N值的增加,输出的S值稳定在某个常数上.这个常数是