题目内容
已知椭圆C的中心坐标在原点，焦点在x轴上，椭圆C上的点到焦点距离的最大值为3，最小值为1。
（1）求椭圆C的标准方程；
（2）若直线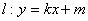
与椭圆C相交于A、B两点（A，B不是左右顶点），且以AB为直径的圆过椭圆C的右顶点，求证：直线l过定点，并求出该定点的坐标 。
解：（1）由题意设椭圆的标准方程为
由已知得：
椭圆的标准方程为
…………（5分）
（2）设
联立
得
…………（7分）
…………（9分）
因为以AB为直径的圆过椭圆的右焦点D（2，0）
∴
∴
+ 
-2
∴
∴
解得：
且均满足
…………（11分）
当
，直线过定点（2，0）与已知矛盾……（12分）
当
时，l的方程为
，直线过定点（
，0）
所以，直线l过定点，定点坐标为（，0） …………（13分）
练习册系列答案
阅读快车系列答案
相关题目
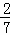，现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取…，取球后不放回，直到两人中有一人取到白球时终止，每个球在每一次被取出的机会是等可能的，用ξ表示取球终止所需要的取球次数．
的右焦点，且与直线
相切的圆方程是 ________；
表示不超过实数
的最大整数
，如：
．定义
，求
（ ）
，则极点到该直线的距离是 
）6的展开式中常数项为 （用数字作答）．
的展开式的各项系数的和为
，所有二项式系数的和为
，则
的值为 ．
，则∁RA =( )
,0] B. (-