题目内容
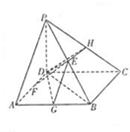
 如图,四棱锥P-ABCD的底面是边长为2的正方形,PD⊥底面ABCD,PD=CD,E为PB的中点.
如图,四棱锥P-ABCD的底面是边长为2的正方形,PD⊥底面ABCD,PD=CD,E为PB的中点.(Ⅰ)求异面直线PA与DE所成的角;
(Ⅱ)在底边AD上是否存在一点F,使EF⊥平面PBC?证明你的结论.
考点:直线与平面垂直的判定,异面直线及其所成的角
专题:空间位置关系与距离
分析:(Ⅰ)取AB的中点G,连结EG、DG,由EG∥PA,∠DEG为所求的角,由此能求出异面直线PA与DE所成角.(Ⅱ)存在点F为AD的中点,使EF⊥平面PBC.取PC的中点H,连结DH,EH,由已知条件推导出四边形EFDH是平行四边形,从而EF∥DH,由此得到EF⊥平面PBC.
解答:
解:(Ⅰ)取AB的中点G,连结EG、DG,∵E是PB的中点,
∴EG∥PA,∴∠DEG为所求的角,
由已知得BD=2
,PD=2,则PB=2
,
∴DE=
PB=
,
又EG=
PA=
,DG=
=
,
∴DG2=DE2+EG2,∴∠DEG=90°,
∴异面直线PA与DE所成角为90°.
(Ⅱ)存在点F为AD的中点,使EF⊥平面PBC.
证明如下:
取PC的中点H,连结DH,EH,
∵PD=CD,∴DH⊥PC,①
∵PD⊥底面ABCD,∴PD⊥BC,
∵底面ABCD是正方形,∴CD⊥BC,
∴BC⊥平面PCD,∴BC⊥DH.②
结合①②知DH⊥平面PBC,
∵E,F分别是PB、AD的中点,
∴FD
BC,EH
BC,∴FD
EH,
∴四边形EFDH是平行四边形,∴EF∥DH,
∴EF⊥平面PBC.
∴EG∥PA,∴∠DEG为所求的角,
由已知得BD=2
| 2 |
| 3 |

∴DE=
| 1 |
| 2 |
| 3 |
又EG=
| 1 |
| 2 |
| 2 |
| AD2+AG2 |
| 5 |
∴DG2=DE2+EG2,∴∠DEG=90°,
∴异面直线PA与DE所成角为90°.
(Ⅱ)存在点F为AD的中点,使EF⊥平面PBC.
证明如下:
取PC的中点H,连结DH,EH,
∵PD=CD,∴DH⊥PC,①
∵PD⊥底面ABCD,∴PD⊥BC,
∵底面ABCD是正方形,∴CD⊥BC,
∴BC⊥平面PCD,∴BC⊥DH.②
结合①②知DH⊥平面PBC,
∵E,F分别是PB、AD的中点,
∴FD
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
∴四边形EFDH是平行四边形,∴EF∥DH,
∴EF⊥平面PBC.
点评:本题考查异面直线所成角的大小的求法,考查直线与平面垂直的判断,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
若函数y=sinx的图象上的每个点的纵坐标不变,将横坐标缩小为原来的
,再将图象沿x轴向右平移
个单位,则新图象对应的函数式是( )
| 1 |
| 3 |
| π |
| 3 |
| A、y=-sin3x | ||||
B、y=sin(
| ||||
C、y=sin(3x-
| ||||
D、y=sin(3x-
|

 已知y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<
已知y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<