题目内容
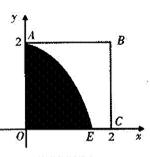
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路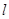 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数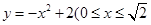 的图象,且点M到边OA距离为
的图象,且点M到边OA距离为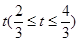 .
.
(1)当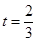 时,求直路
时,求直路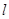 所在的直线方程;
所在的直线方程;
(2)当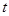 为何值时,地块OABC在直路
为何值时,地块OABC在直路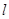 不含泳池那侧的面积取到最大,最大值是多少?
不含泳池那侧的面积取到最大,最大值是多少?
(1)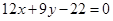 ;(2)
;(2)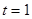 时,
时,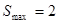 .
.
解析试题分析:(1)点M到边OA距离为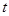 ,则可设
,则可设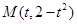 ,当
,当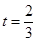 时,求切线的方程是一个常规问题,切线的斜率是
时,求切线的方程是一个常规问题,切线的斜率是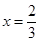 处的导数,易求出直线的点斜式方程;(2)要求不含泳池一侧的面积,就是要把这个面积表示为变量
处的导数,易求出直线的点斜式方程;(2)要求不含泳池一侧的面积,就是要把这个面积表示为变量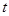 的函数,为此需要确定切线与线段
的函数,为此需要确定切线与线段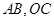 的交点,当然也可能是与线段
的交点,当然也可能是与线段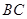 的交点,这作一个判断或分类讨论,面积函数解决后,用一般求最值的方法,则可解决问题.
的交点,这作一个判断或分类讨论,面积函数解决后,用一般求最值的方法,则可解决问题.
试题解析:
(1)对函数 求导得,
求导得,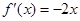 ,
,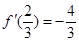 ,又
,又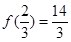 ,所以切点
,所以切点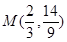 ,切线
,切线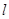 的方程为
的方程为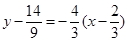 ,即
,即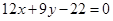 ;
;
(2)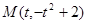 ,过切点
,过切点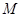 的切线
的切线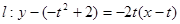
即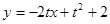 ,令
,令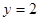 得
得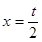 ,故切线
,故切线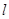 交
交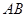 于点
于点 ;
;
令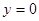 ,得
,得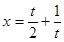 ,又
,又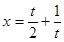 在
在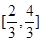 递减,所以
递减,所以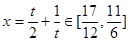
故切线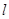 与OC交于点
与OC交于点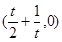 。
。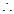 地块OABC在切线
地块OABC在切线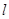 右上部分区域为直角梯形,
右上部分区域为直角梯形,
面积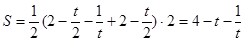
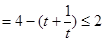 ,当
,当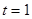 ,
,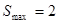 。
。
考点:导数的应用、函数的最值.

练习册系列答案
相关题目
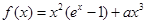
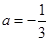 时,求
时,求 的单调区间;
的单调区间;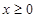 时
时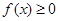 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。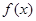 为定义域
为定义域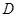 上的单调函数,且存在区间
上的单调函数,且存在区间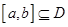 (其中
(其中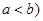 ,使得当
,使得当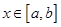 时,
时, 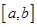 ,则称函数
,则称函数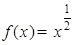 是
是 上的正函数,求
上的正函数,求 的等域区间;
的等域区间; ,使得函数
,使得函数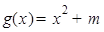 是
是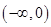 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数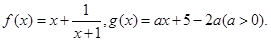
 在
在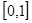 上的单调性,并用定义加以证明;
上的单调性,并用定义加以证明;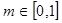 ,总存在
,总存在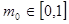 ,使得
,使得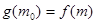 成立,求实数
成立,求实数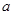 的取值范围
的取值范围 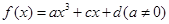 是R上的奇函数,当
是R上的奇函数,当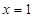 时
时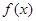 取得极值
取得极值 .
.
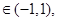 不等式
不等式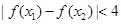 恒成立.
恒成立. ,
, 为自然对数的底,
为自然对数的底, 的最值;
的最值;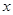 方程
方程 有两个不同解,求
有两个不同解,求 的范围.
的范围.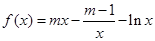 ,
, 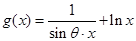 在
在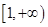 上为增函数,且
上为增函数,且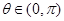 ,求解下列各题:
,求解下列各题: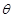 的取值范围;
的取值范围;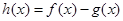 在
在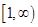 上为单调增函数,求
上为单调增函数,求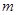 的取值范围;
的取值范围;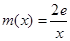 ,若在
,若在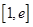 上至少存在一个
上至少存在一个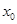 ,使得
,使得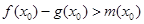 成立,求
成立,求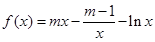 ,
, 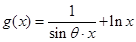 在
在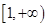 上为增函数,且
上为增函数,且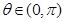 ,求解下列各题:
,求解下列各题: 的取值范围;
的取值范围; 在
在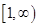 上为单调增函数,求
上为单调增函数,求 的取值范围;
的取值范围;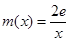 ,若在
,若在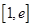 上至少存在一个
上至少存在一个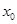 ,使得
,使得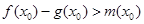 成立,求
成立,求 .
. ,
, 时,求函数
时,求函数 的最大值;
的最大值; ,其图象上存在一点
,其图象上存在一点 ,使此处切线的斜率
,使此处切线的斜率 ,求实数
,求实数 的取值范围;
的取值范围; ,
, ,
, 时,方程
时,方程 有唯一实数解,求
有唯一实数解,求 的值.
的值.