题目内容
已知圆的方程是:![]() ,其中
,其中![]() ,且
,且![]() 。
。
(1)求证:![]() 取不为1的实数时,上述圆恒过定点;(2)求与圆相切的直线方程;(3)求圆心的轨迹方程。
取不为1的实数时,上述圆恒过定点;(2)求与圆相切的直线方程;(3)求圆心的轨迹方程。
解:将方程![]() 整理得:
整理得:
![]() 令
令
解之得:![]() ∴定点为(1,1);-------------------------------------4分
∴定点为(1,1);-------------------------------------4分
(2)易得已知圆的圆心坐标为![]() ,半径为
,半径为![]()
![]() 。
。
设所求切线方程为![]() ,即
,即![]() ,
,
则圆心到直线的距离应等于圆的半径,即![]() =
=![]()
![]() 恒成立。
恒成立。
整理得等式:![]()
![]() 恒成立。
恒成立。
比较系数可得:
解之得![]() ,所以,所求的切线方程是
,所以,所求的切线方程是![]() 。------------9分
。------------9分
(3)圆心坐标为![]() ,又设圆心坐标为
,又设圆心坐标为![]() ,则有:
,则有:
![]() 消去参数得
消去参数得![]() 为所求的圆心的轨迹方程。
为所求的圆心的轨迹方程。

练习册系列答案
相关题目
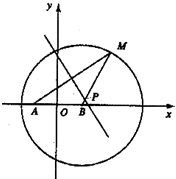 (2003•崇文区一模)已知圆B方程(x-c)2+y2=4a2(a>c>0,a,c是常数),且A(-c,0),点M在圆B上运动,线段AM的垂直平分线交MB于点P.
(2003•崇文区一模)已知圆B方程(x-c)2+y2=4a2(a>c>0,a,c是常数),且A(-c,0),点M在圆B上运动,线段AM的垂直平分线交MB于点P.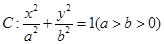 的离心率为
的离心率为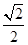 ,其左、右焦点分别为
,其左、右焦点分别为 ,点
,点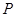 是椭圆上一点,且
是椭圆上一点,且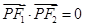 ,
,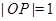 (
(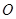 为坐标原点).
为坐标原点).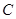 的方程;
的方程;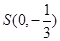 且斜率为
且斜率为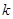 的动直线
的动直线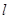 交椭圆于
交椭圆于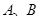 两点,在
两点,在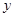 轴上是否存在定点
轴上是否存在定点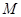 ,使以
,使以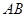 为直径的圆恒过这个点?若存在,求出
为直径的圆恒过这个点?若存在,求出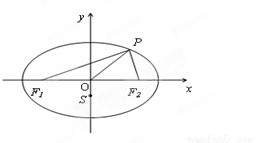
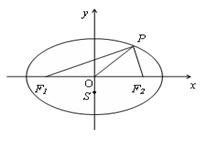
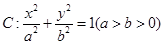 的离心率为
的离心率为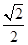 ,其左、右焦点分别为
,其左、右焦点分别为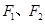 ,点
,点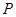 是椭圆上一点,且
是椭圆上一点,且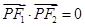 ,
,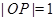 (
(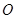 为坐标原点).
为坐标原点).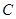 的方程;
的方程;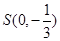 且斜率为
且斜率为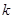 的动直线
的动直线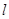 交椭圆于
交椭圆于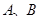 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点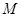 ,使以
,使以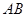 为直径的圆恒过这个点?若存在,求出
为直径的圆恒过这个点?若存在,求出